Functies en grafieken > TotaalbeeldTesten
Gegeven zijn de functies `f(x)=5 x^2(x+20 )` en `g(x)=50 x^2` .
Bereken algebraïsch de nulpunten van `f` .
Plot de grafieken van `f` en `g` , zodat alle karakteristieken goed te zien zijn.
Schrijf op welke vensterinstellingen je hebt gebruikt.
Bereken de snijpunten van de grafieken van `f` en `g` .
Bereken algebraïsch bij de functies eerst de nulpunten. Bepaal vervolgens het domein en bereik van de functies.
`f(x)=x^2(x^2-400 )`
`g(x)=sqrt(20 -x)-40`
Gegeven is de functie `y(x)=4 -1/x^2` .
Welke asymptoten heeft de grafiek van deze functie?
Geef het domein en bereik van `f` .
Los algebraïsch op: `y=2` . Geef benaderingen in twee decimalen nauwkeurig.
Je ziet vier grafieken die zijn ontstaan door op de grafiek van `f(x)=sqrt(x)` één of meer transformaties toe te passen. Steeds zijn de standaardinstellingen van het venster van de grafische rekenmachine gebruikt.
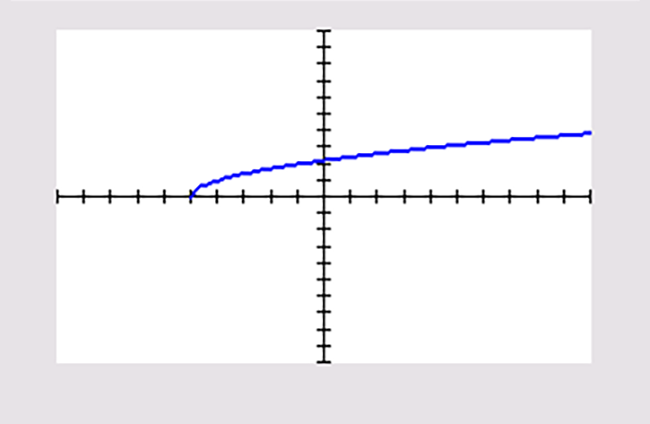
a |
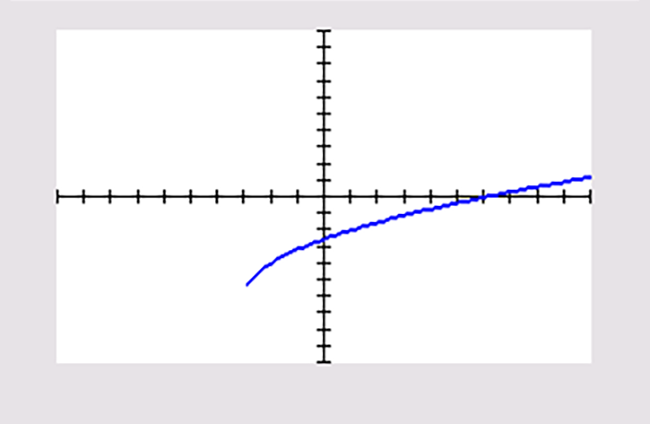
b |
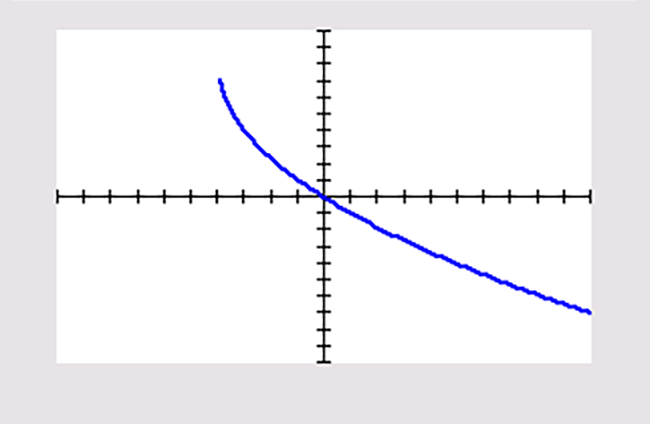
c |
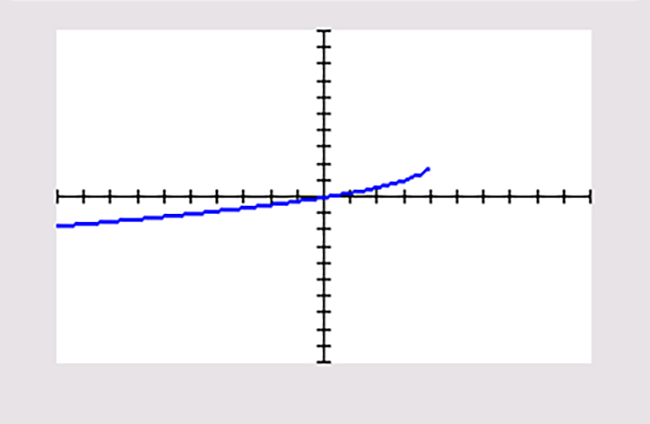
d |
Schrijf bij elke grafiek het juiste functievoorschrift op.
Gegeven is de functie `f` met `f(x)=0,25(x-10 ) ^2-16` .
Door welke transformaties kan de grafiek van `f` ontstaan uit die van `y=x^2` ?
Bepaal de top en de nulpunten van de grafiek van `f` .
Gegeven zijn de functies `f(x)=text(-)2x+4` en `g(x)=text(-)2x-2` .
Geef het functievoorschrift van `h(x)=f(g(x))` .
Geef het voorschrift van `f^(text(inv))` .
In de figuur zie je de grafieken I en II. I is de grafiek van `y=x^3` . Grafiek II ligt rechts van I, zodanig dat alle horizontale verbindingslijnstukken van I en II de lengte `2` hebben.
Geef een bij grafiek II passend functievoorschrift.
De verticale verbindingslijnstukken van I en II variëren in lengte. Bereken de waarden van `x` waarvoor die lengte `26` is.
Bereken de kortste lengte van zo’n verticaal verbindingslijnstuk.