Logaritmen

Logaritmen > Logaritmische schalen

12345Logaritmische schalen

Antwoorden van de opgaven

Opgave V1

`log(T)=log(60*(0,8)^t) = log(60)+log(0,8^t) = log(60)+t*log(0,8)` .

Omdat `log(T) = text(-)0,097t + 1,778` een lineaire functie is.

Maak in GeoGebra de grafiek van `y ~~ text(-)0,097x + 1,778` en zet bij de `x` -as de letter `t` en bij de `y` -as `log(T)` .

Bij `T=10` hoort `log(T) = log(10) = 1` , dus je leest af bij `1` op de `y` -as.

Je vindt `t ~~ 8,03` tijdseenheden.

Opgave 1

`log(B)=log(6 *2^t)=log(6 )+log(2^t)=log(6 )+t*log(2 )`
De grafiek wordt een rechte lijn door `(0 , log(6 ))` en met richtingscoëfficiënt `log(2 )` .

`t`	0	1	2	3	4	5	...	15
`log(B)`	0,78	1,08	1,38	1,68	1,98	2,28	...	5,29

Zie de bovenste figuur in de uitleg.

Nee, op de verticale as zit tussen twee opeenvolgende streepjes steeds een factor `10` . De stappen worden dus steeds groter: van `1` naar `10` is een kleinere afstand dan van `10` naar `100` .

`B(5)=6*2^5=6*32=192` , dus tussen `100` en `1000` .
De juiste plek vind je door de logaritme te berekenen: `log(192)~~2,28` .
Dus het punt moet op `10^(2,28) ~~ 1,9*10^2` zijn getekend en dat klopt ongeveer.

Op vergelijkbare manier is `B(10)=6*2^(10)=6144` en `log(6144)~~3,79` .
Dus het punt moet op `10^(3,79) ~~ 6,2*10^3` zijn getekend en dat klopt ongeveer.

Opgave 2

Het maatstreepje op hoogte `4` zit bij `log(4) ~~ 0,60` en dat klopt ongeveer.

Omdat de grafiek ongeveer een rechte lijn is in een enkellogaritmisch assenstelsel heeft de formule de vorm `B = a*g^t` . Vul hierin beide gegevens is:

`B(2) = a*g^2 = 9`
`B(8) = a*g^8 = 100`

Uit de eerste vergelijking volgt `a = 9/(g^2)` en dit vul je bij de tweede vergelijking in: `9/(g^2)*g^8 = 100` .

Dit levert op: `9 g^6 = 100` en `g^6 = 100/9` zodat `g = (100/9)^(1/6) ~~ 1,49` .

En ook: `a = 9/(g^2) ~~ 4,03` .

Je krijgt op één decimaal nauwkeurig: `B(t) = 4,0*1,5^t` . Dit komt met de gegeven formule overeen.

Opgave 3

`L = k*V^p` geeft `log(L) = log(k*V^p)` .
Met de rekenregels wordt dit `log(L) = log(V^p) + log(k)` en `log(L) = p*log(V) + log(k)` .

Neem je `p=a` en `log(k)=b` dan krijg je `log(L) = log(V^p) + log(k)` .

De grafiek is een rechte lijn in een assenstelsel met op beide assen een logaritmische schaalverdeling.

Gebruik bijvoorbeeld `L(40)=1,92` en `L(160)=30,72` .

Invullen in `L = k*V^p` geeft `1,92 = k*40^p` en `30,72 = k*160^p` .

De eerste vergelijking geeft `k = (1,92)/(40^p)` .

Dit invullen in de tweede geeft `30,72 = (1,92)/(40^p)*160^p` en `4^p = 16` .

Dus `p=2` en `k = (1,92)/(40^p) = 0,0012` .

De gevraagde formule wordt: `L = 0,0012*V^2` .

Opgave 4

`A(2 )≈120`
`A(10 )≈1800`

`A(t)=63*1,4^t`

Omdat je dan meteen kunt aflezen welke waarde `b` heeft.

Opgave 5

`(0; 0,001 )`

Gebruik bijvoorbeeld de punten `(text(-)4, 1000)` en `(5; 0,01)` . Je vindt dan de formule `N(t)≈6 *0,28^t` .

`(6,83 ; 0,001)`

`N(t)>0` voor elke `t` .

Opgave 6

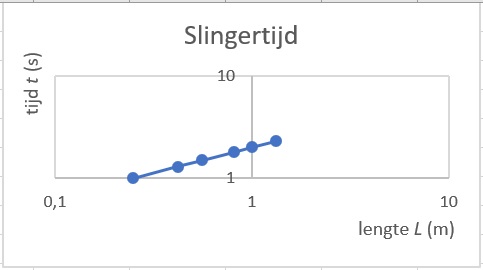
Gebruik bijvoorbeeld het dubbellogaritmisch grafiekenpapier.
Of zet `log(L)` tegen `log(t)` uit op gewoon grafiekenpapier.
Hiernaast zie je wat Excel doet.

`L(0,25) = 1,0` en `L(1,00) = 2,0` geven `1,0 = c*0,25^p` en `2,0 = c*1^p` .
Uit de laatste volgt `c = 2,0` en dat betekent `1,0 = 2,0*0,25^p` ofwel `0,25^p = 0,5` .
En daar mee is `p = \ ^(0,25)log(0,5) = 0,5` .

En inderdaad krijg je `t ~~ 2,0*L^(0,5)` .

`t = 2pi*sqrt(L/g) = (2pi)/(sqrt(9,8))*sqrt(L) ~~ 2,0 * L^(0,5)` .

Opgave 7

De grafiek gaat door de punten die horen bij de kat en het paard.
Dus `Z(4)=2` en `Z(750)=100` .
Vul deze gegevens in `Z = c*m^p` in: `2 = c*4^p` en `100 = c*750^p` .
Hieruit volgt `100 = 2*(750/4)^p` en dus `p ~~ 0,75` .
En verder `c = 2/(4^(0,75)) ~~ 0,70` .

Dus krijg je inderdaad `Z = 0,70*m^(0,75)` .

`Z = 0,70*500^(0,75) ~~ 74` L/uur.

Opgave 8

Voor `V(t)=b*g^t` geldt:

`V(0 )=b*g^0=3`
`V(6 )=b*g^6=7`

Dit levert: `b=3` en `g^6=7/3=2 1/3` , zodat `g=(2 1/3)^(1/6)≈1,15` .
Een passende formule is dan `V(t)≈3 *1,15^t` .

Los op: `V(t)=5`

`3*1,15^t`	`=`	`5`
`1,15^t`	`=`	`1 2/3`
`t`	`=`	`\ ^(1,15)log(1 2/3)≈3,65`

`t` -as ligt op hoogte `1`
Los op: `V(t)=1`

`3*1,15^t`	`=`	`1`
`1,15^t`	`=`	`1/3`
`t`	`=`	`\ ^(1,15)log(1/3)≈text(-)7,86`

Opgave 9

`t`	0	1	2	3	4	5	6
`log(N)`	1,70	1,92	2,15	2,37	2,60	2,83	3,05

Ja, je krijgt ongeveer een rechte lijn door `(0 ; 1,70 )` en `(4 ; 2,60 )` .

Ja er is sprake van exponentiële groei.

`log(N)≈1,70 +0,22 t`

`N(t)=50 *1,66^t`

Opgave 10

De punten liggen bij benadering op een rechte lijn op dubbellogaritmisch papier. Er is sprake van een machtsverband tussen `x` en `y` .

Het model wordt gegeven door `y=a*x^b` .
Als `x=1` , dan is `y=35` . Hieruit volgt dat `a=35` .
Als `x=5` , dan is `y=78` . Hieruit volgt `78=35*5^b` .
De grafische rekenmachine geeft `b≈0,5` . Het model wordt `y=35*x^(0,5)` .
Als `x=1000` , dan is `y≈1107` . (Eventueel kun je dit ook proberen af te lezen van het dubbellogpapier.)

Opgave 11

De lijn gaat door de punten `(log(h), w) =(0, 2)` en `(log(h), w)=(2, 8)` .

De helling is dan `a=(8-2)/(2-0)=3` .

Invullen van `(2, 8)` levert je de waarde van `b` : `8=3*log(100)+b` . Dus `b=2` .

Het startgetal is dan gelijk aan `2` .

Opgave 12

`log(m)≈0,1` en `log(P)≈2,4` .

`log(P)≈text(-)0,14 *log(m)+2,41` .

`P~~ 257 *m^(text(-)0,14)`

Opgave A1Van ruitjespapier naar logaritmisch papier

Van ruitjespapier naar logaritmisch papier

Van decimale waarden `rarr` log-waarden	Van log-waarden `rarr` afstanden
` 1=10^x hArr x=\ ^10log(1) =0 rArr 10^0 =1`	`0 *10` cm `=0` cm
` 2=10^x hArr x=\ ^10log(2) =0,3 rArr 10^(0,3) =2`	`0,3 *10` cm `=3` cm
` 3=10^x hArr x=\ ^10log(3) =0,48 rArr 10^(0,48)=3`	`0,48*10` cm `=4,8` cm
` 4=10^x hArr x=\ ^10log(4) =0,6 rArr 10^(0,6) =4`	`0,6 *10` cm `=6` cm
` 5=10^x hArr x=\ ^10log(5) =0,7 rArr 10^(0,7) =5`	`0,7 *10` cm `=7` cm
` 6=10^x hArr x=\ ^10log(6) =0,78 rArr 10^(0,78)=6`	`0,78*10` cm `=7,8` cm
` 7=10^x hArr x=\ ^10log(7) =0,85 rArr 10^(0,85)=7`	`0,85*10` cm `=8,5` cm
` 8=10^x hArr x=\ ^10log(8) =0,9 rArr 10^(0,9) =8`	`0,9 *10` cm `=9` cm
` 9=10^x hArr x=\ ^10log(9) =0,92 rArr 10^(0,92)=9`	`0,92*10` cm `=9,2` cm
`10=10^x hArr x=\ ^10log(10)=1 rArr 10^1 =10`	`1 *10` cm `=10` cm

De figuur is het antwoord op b en c.

Zie figuur bij b.

Opgave A2Formule van een machtsverband afleiden uit een grafiek

Formule van een machtsverband afleiden uit een grafiek

`p`	`=`	`a*V^m`	beide kanten logaritme nemen
`log p`	`=`	`log (a*V^m)`	rekenregel logaritme toepassen: `log(M)+log(N)=log(M*N)`
`log p`	`=`	`log a+log V^m`	rekenregel logaritme toepassen: `n*log(M)=log(M^n)`
`log p`	`=`	`log a+m*log V`

Vergelijk dit met de vergelijking van een rechte lijn: `y=A*x+B` .
Nu staat langs de assen echter `log(p)` en `log(V)` dus `m` komt overeen met `A` (de richtingscoëfficiënt, ofwel helling van de lijn).

`V` (dm³)	`p` (N/m²)	`log(V)`	`log(p)`	`ΔV` (in cm)	`Δp` (in cm)
`4`	`15*10^4`	`0,6`	`5,18`	`6`	`1,8`
`3`	`19*10^4`	`0,48`	`5,28`	`4,8`	`2,8`
`2`	`30*10^4`	`0,3`	`5,48`	`3`	`4,8`
`1,5`	`41*10^4`	`0,18`	`5,61`	`1,8`	`6,1`

Voor de helling van de lijn geldt `m=(text(-)8)/(7,7)~~text(-)1,04.`
De " `y` -coördinaat" van punt `S` is de beginwaarde van de machtsfunctie. Dit is `log(p)` bij `log(V)=1` . Door te meten (schaaldeel) volgt `a=10^(5,8)~~6,3*10^5` .
De vergelijking van de machtsfunctie is `p=6,3*10^5*V^(text(-)1,04)` .

Opgave T1

Bekijk de figuur.

Er is sprake van exponentiële groei.

`N(t)=40 *1,495^t` met `t` in weken.

Opgave T2

Er is geen sprake van een exponentieel verband, de punten liggen op enkellogaritmisch papier niet op een rechte lijn.

Er is sprake van een machtsverband, de punten liggen op dubbellogaritmisch papier bij benadering op een rechte lijn.

De rechte lijn gaat ongeveer door `(10^2; 2,8)` en `(10^3, 12)` .

De formule wordt dan `H~~0,15*G^(0,63)` .

De afwijkingen hebben met het aflezen te maken.

Los de ongelijkheid `0,12*G^(0,67)>150` op.

Het lichaamsgewicht van een zoogdier met een hersengewicht van meer dan `150` gram is meer dan `41903` gram.

verder | terug