Voorbeeld 2
De slingertijd `t` (in s) is de tijd die een gewicht dat aan een touw is opgehangen en aan het heen en weer slingeren wordt gebracht nodig heeft voor één heen- en weer gaande beweging. Die slingertijd hangt af van de lengte `L` (in m) van het touw. Hier zie je enkele meetgegevens:
| `L` in m | `0,25` | `0,42` | `0,56` | `0,81` | `1,00` | `1,32` |
| `t` in s | `1,0` | `1,3` | `1,5` | `1,8` | `2,0` | `2,3` |
Laat zien dat een bijpassende grafiek met op beide assen een logaritmische schaalverdeling ongeveer een rechte lijn oplevert en stel een bijpassende formule op.
De grafiek kun je op verschillende manieren maken:
-
De tabel uitbreiden met rijen voor `log(L)` en `log(t)` .
Vervolgens zet je in een assenstelsel met gewone lineaire schaalverdelingen `log(L)` tegen `log(t)` uit. -
De tabel in Excel invoeren en een spreidingsgrafiek maken.
Vervolgens kies je op beide assen een logaritmische schaalverdeling. -
Een blad dubbellogaritmisch papier gebruiken.
De grafiek moet in alle gevallen ongeveer een rechte lijn worden.
Je weet dan dat de bijbehorende formule de vorm `t = c*L^p` moet hebben.
Lees twee punten op de lijn af, bijvoorbeeld `L(0,25) = 1,0` en `L(1,00) = 2,0` .
Vul je deze waarden in de formule in, dan kun je `c` en `p` berekenen.
Je vindt: `t ~~ 2,0*L^(0,5)` .
In Voorbeeld 2 vind je de gegevens van de slingertijd `t` afhankelijk van de slingerlengte `L` .
Maak een bijbehorende grafiek met op beide assen een logaritmische schaalverdeling.
Stel zelf de formule op die in het voorbeeld staat.
Laat zien, dat dit in overeenstemming is met de uit de natuurkunde bekende formule
`t = 2pi*sqrt(L/g)`
.
Hierin is
`g ~~ 9,8`
.
Bekijk deze tabel en bijbehorende grafiek van het zuurstofverbruik `Z` (in liter/uur) afgezet tegen de lichaamsmassa `m` in kg.
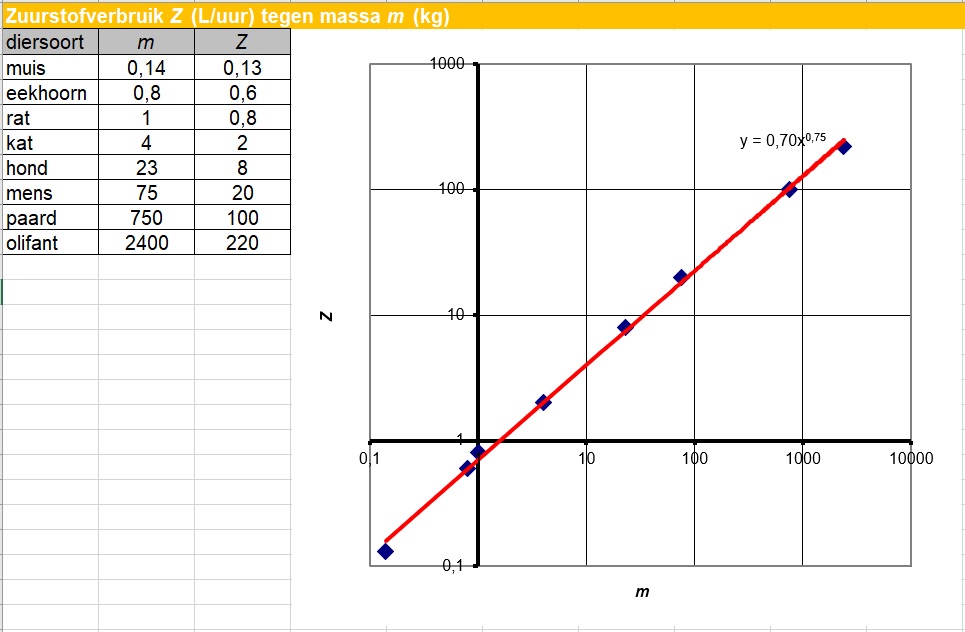
Door de punten is ongeveer een rechte lijn te trekken.
Laat door berekening zien, dat bij deze lijn inderdaad de formule
`Z = 0,70*m^(0,75)`
hoort.
De massa van een koe bedraagt `500` kg. Hoeveel bedraagt het zuurstofverbruik?