Formules opstellen

Formules opstellen > Totaalbeeld

12345Totaalbeeld

Toepassen

Opgave A1Eerste-orde processen

Eerste-orde processen

In de procesindustrie komen zogenaamde eerste-orde processen veel voor. Kenmerkend voor dit type processen is dat de proceswaarde exponentieel verandert in de tijd. Een simpel voorbeeld is het afkoelingsproces van een vloeistof waarvan de temperatuur hoger is dan de omgevingstemperatuur, een kop koffie bijvoorbeeld.
Neem als voorbeeld het afkoelingsproces, daarvan kun je het verloop van de temperatuur $T$ in de tijd beschrijven met de volgende formule:

$T(t) = T_0 - Delta T * (1 - text(e)^(text(-)t/(tau)))$

Hierin is:

$T$ de temperatuur op tijdstip $t$
$T_0$ de temperatuur op tijdstip $t = 0$
$Delta T$ het temperatuurverschil tussen de begintemperatuur $T_0$ en de omgevingstemperatuur ( $T_0 - T_(text(omgeving))$ )
$tau$ de tijdconstante of traagheid van het proces (spreek uit als "tau")
$text(e)$ het getal van Euler $text(e) ~~ 2,718$

Let wel: Het temperatuurverschil $Delta T$ is de drijvende kracht achter het proces, het zorgt ervoor dat er een warmtestroom op gang komt. Hierdoor wordt $Delta T$ steeds kleiner en op gegeven moment gelijk aan nul: er is een nieuwe evenwichtstoestand bereikt als de drijvende kracht is weggevallen!
Bijgaande figuur is een voorbeeld van het verloop van de temperatuur in de tijd bij een afkoelingsproces.

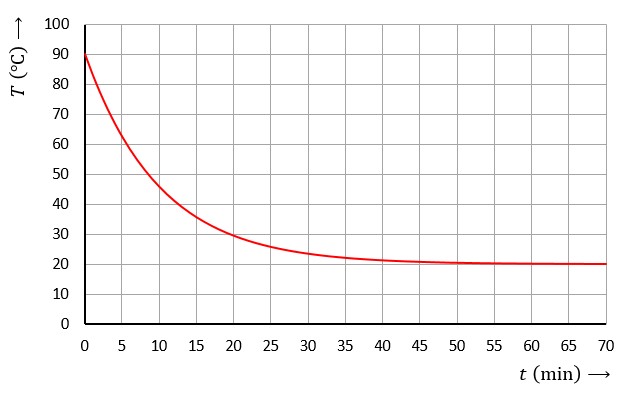
Eén van de methoden om de tijdconstante $tau$ van het proces te achterhalen, staat bekend als de $63$ % methode. Pas deze toe via de volgende stappen:

Bereken hoe groot $63$ % van de totale verandering ( $Delta T$ ) is.
Reken uit bij welke temperatuur je uitkomt als deze $63$ % verandering is bereikt.
Het bijbehorende tijdstip is dan de tijdconstante $tau$ van het proces. Bepaal deze tijdconstante zo nauwkeurig mogelijk.

Bereken de temperatuur van de koffie na $20$ minuten.

Aangezien je nu over een formule beschikt die het verloop van de temperatuur in de tijd beschrijft, kun je ook uitrekenen hoe lang het zal duren alvorens een bepaalde temperatuur is bereikt.

Reken uit hoe lang het duurt voordat de temperatuur is gedaald tot $25$ °C. Klopt dit met de grafiek?

Opgave A2Pendule

Pendule

In bijgaande figuur is een slinger weergegeven. Als je de lengte $l$ van de slinger verandert, dan verander je daarmee ook de slingertijd $T$ . Iemand heeft een aantal metingen van de slingertijd (of periode) voor een aantal verschillende slingerlengten gedaan. De resultaten staan in onderstaande tabel.

Lengte $l$ (in m)	$0,5$	$0,6$	$0,7$	$0,8$	$0,9$	$1,0$
Periode $T$ (in s)	$1,42$	$1,55$	$1,68$	$1,80$	$1,90$	$2,01$

Maak je hierbij een grafiek dan blijkt dat $T$ niet recht evenredig is met $l$ .

Leg eens uit waarom $T$ ook niet evenredig is met $l^2$ of $l^3$ ?

Toch is het verband tussen $T$ en $l$ een machtsverband van de vorm $T(l) = a * l^b$ .

Laat zien, hoe je zelf de bijpassende waarden voor $a$ en $b$ kunt bepalen.

Misschien ken je de bekende formule $T = 2π sqrt(l/g)$ voor het verband tussen de lengte en de periode van een slinger wel. Hierin is $g=9,8$ m/s².

Kloppen de gevonden waarden van $a$ en $b$ met de deze formule?

| Testen