Exponenten en machten > MachtsfunctiesVoorbeeld 3
Los op in twee decimalen nauwkeurig: `2/ ((x+1)^4) gt 4` .
Omdat
`f(x)=2/(x+1)^4=2*(x+1)^(text(-)4)`
is ook hier sprake van een machtsfunctie.
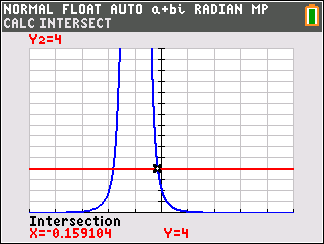
Maak eerst de grafiek van
`f`
en de lijn
`y_2 =4`
.
Los nu op: `2*(x+1)^(text(-)4)=4` .
Oplossing: `x=text(-)1 + 2^(text(-) 1/4) ~~ text(-)0,159 ∨ x=text(-)1 - 2^(text(-) 1/4)~~text(-)1,841` .
In de grafiek is de oplossing van de ongelijkheid af te lezen: `text(-) 1,84 lt x lt text(-)1 ∨ text(-)1 lt x le text(-)0,16` .
Merk op dat je `x=text(-)1` uitzondert omdat voor deze waarde de functie `f` niet bestaat.
Los de volgende vergelijkingen en ongelijkheden algebraïsch op. Controleer je antwoord met de grafische rekenmachine. Houd ook rekening met het domein van de verschillende functies.
`x^2 lt sqrt(x)`
`1/(x^4)=81`
`1/(x^3) lt 27`
`1/x^3 lt 30`
`x^5 lt x^4`
`x^6 lt x^4`
Gegeven is de functie `f(x)=2 (x+1 ) ^(text(-)2)-4` .
Welke asymptoten heeft de grafiek van `y=x^(text(-)2)` ?
Beschrijf welke transformaties je moet uitvoeren op de grafiek van `y=x^(text(-)2)` om die van `f` te krijgen.
Welke asymptoten heeft de grafiek van `f` ?
Schrijf domein en bereik van `f` op.
Los op: `f(x) lt 10` .