Differentiëren > De product- en de quotiëntregelToepassen
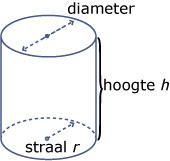
Een blikfabriek maakt onder andere cilindervormige blikken voor de conservenindustrie. Er is veel vraag naar blikken met een inhoud van `1` liter. Voor de fabrikant is het belangrijk dat daar zo min mogelijk blik voor nodig is, dan blijven zijn kosten laag.
Voor het volume
`V`
van zo'n blik geldt
`V = pi r^2 h`
.
Voor de oppervlakte aan blik geldt
`A = 2pi r^2 + 2pi rh`
.
Neem alle afmetingen in cm en laat zien, dat `h = 1000/(pi r^2)`
Stel een formule op voor de blikoppervlakte `A` als functie van `r`
Bereken voor welke waarde van `r` de blikoppervlakte minimaal is.
Op rechthoekige vellen papier van
`1`
m2 worden foto’s afgedrukt om posters te maken. Om de foto blijft een rand wit: aan de onderkant een strook van
`2`
dm breedte, aan de andere drie randen stroken van
`1`
dm breedte.
Bij welke afmetingen van de poster wordt de oppervlakte van het bedrukte deel zo groot mogelijk?
Maak zelf een schets van de situatie met de gegevens er in.
Probeer eerst zelf het probleem op te lossen. Kijk pas als dat niet lukt naar c en d.
Neem aan dat de breedte van zo’n poster wordt voorgesteld door `x` dm. Leid een formule af voor de oppervlakte `A` van het bedrukte deel als functie van `x` .
Bereken met behulp van differentiëren de waarde van `x` waarvoor `A(x)` maximaal is.
Beantwoord tenslotte de aan het begin gestelde vraag.