Lineaire verbanden > Lineaire verbandenVoorbeeld 1
Een museum trok op een zaterdag veel bezoekers. Een kinderkaartje kostte € 1,50 en een kaartje voor volwassenen kostte € 2,50. In totaal is er voor € 1245,00 aan inkomsten door de kaartverkoop. Hoeveel kinderen en hoeveel volwassenen hebben het museum bezocht?
Er zijn meerdere combinaties mogelijk. Bijvoorbeeld `50` kinderen en `468` volwassenen of `150` kinderen en `408` volwassen. Met een grafische rekenmachine of met GeoGebra of Desmos kun je gemakkelijk alle oplossingen bepalen.
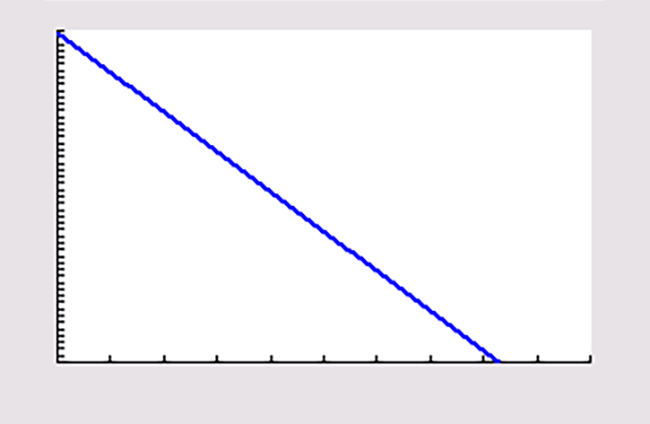
Noem het aantal kinderen
`x`
en het aantal volwassenen
`y`
, dan geldt:
`1,50 x+2,50 y=1245`
. Dit is een lineair verband tussen
`x`
en
`y`
.
Je kunt de formule herleiden tot
`y = 498 - 0,6x`
.
Maak je nu een grafiek of een tabel, dan krijg je alle
mogelijke combinaties van
`x`
en
`y`
.
Je kunt dan de volgende waarden vrij snel vinden:
`x=0`
en
`y=498`
,
`x=5`
en
`y=495`
,
`x = 10`
en
`y = 492`
, ..., tot aan
`x=830`
en
`y=0`
.
Bekijk Voorbeeld 1. Je ziet een lineair verband tussen de variabelen `x` en `y` gegeven door `1,50x+2,50y=1245` .
Laat zien dat je deze formule kunt herleiden tot `y=text(-)0,6x+498` .
Kunnen er `300` kinderen bij de voorstelling aanwezig zijn geweest? Licht je antwoord toe.
Een marktkoopman verkoopt grote en kleine vazen. Grote vazen verkoopt hij voor € 12,00 en de kleine voor € 5,00. Op een dag heeft hij voor € 240,00 aan vazen verkocht.
Hoeveel kleine en grote vazen kan hij verkocht hebben? Schrijf alle combinaties op.
Stel dat de marktkoopman `34` vazen op die dag heeft verkocht. Hoeveel kleine en hoeveel grote vazen heeft hij dan verkocht?