Exponenten en machten > Exponentiële groeiVoorbeeld 1
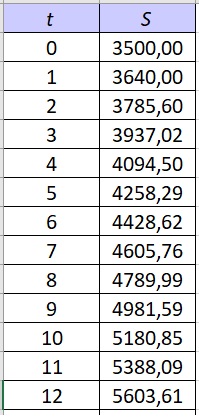
Op 1 januari 2010 stond een bedrag van € 3500,00 op een spaarrekening. De bank gaf op deze rekening een rente van `4` % per jaar. Neem aan dat dit alles vanaf 1 januari 2010 niet is veranderd en stel een formule op voor het saldo `S` op deze rekening afhankelijk van de tijd `t` in jaren vanaf 1 januari 2010. Maak ook een tabel die laat zien hoe het saldo zich ontwikkelde.
Bij een toename van `4` % per jaar hoort een groeifactor van `1,04` .
Op `t=0` was het saldo € 3500,00. Een passende formule is daarom: `S=3500 *1,04^t` .
Als je deze formule invoert in een spreadsheet heb je snel een tabel.
Je kunt ook een grafische rekenmachine gebruiken.
Hoeveel bedraagt de groeifactor bij de genoemde groeipercentages?
`10` % toename
`100` % toename
`0,2` % toename
`100` % afname
`0,1` % afname
`40` % afname
Iemand zet op 1 januari 2010 € 800,00 op een bankrekening tegen `6` % rente. De rente wordt jaarlijks op de bankrekening bijgeschreven. Er wordt verder geen geld op de bankrekening gestort of geld van de bankrekening gehaald.
Wat is de groeifactor per jaar van het tegoed op de bankrekening?
Hoeveel geld staat er op de bankrekening op 1 januari 2015?
Welke formule geldt voor het spaartegoed `S(t)` , waarin `t` de tijd in jaren na 1 januari 2010?
Hoe groot is de groeifactor per vijf jaar? Bereken ook het groeipercentage per vijf jaar.
Laat met berekeningen zien dat je op de volgende manieren het tegoed op 1 januari 2030 kunt berekenen.
-
`t=20` invullen in de formule;
-
het tegoed op 1 januari 2010 vijf keer vermenigvuldigen met de groeifactor per `4` jaar;
-
het tegoed op 1 januari 2010 vier keer vermenigvuldigen met de groeifactor per `5` jaar.