Exponenten en machten > Exponentiële groeiVoorbeeld 2
Een krant ziet in een reeks van jaren het aantal abonnementen dalen.
| jaartal | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| aantal abonnementen ( `xx` 1000) | 970 | 941 | 913 | 885 | 859 | 833 |
Stel op grond van deze tabel een zo goed mogelijk passende formule op die het verloop van het aantal duizenden abonnementen `A` als functie van de tijd `t` in jaren beschrijft. Neem `t=0` voor 2010 . Als het aantal abonnementen onder de `500000` zakt, raakt de krant in problemen. In welk jaar is dat het geval als dit verloop niet wijzigt?
Controleer eerst of je een exponentiële formule mag maken: de jaartallen nemen gelijkmatig toe. Deling van opeenvolgende aantallen abonnementen levert steeds (ongeveer) `0,97` op, dus de daling is een vorm van exponentiële groei.
De groeifactor
`g≈0,97 < 1`
, dus er is sprake van exponentiële afname. Het
aantal abonnementen neemt jaarlijks met
`3`
% af.
Een passende formule is daarom:
`A(t)=970 *0,97^t`
.
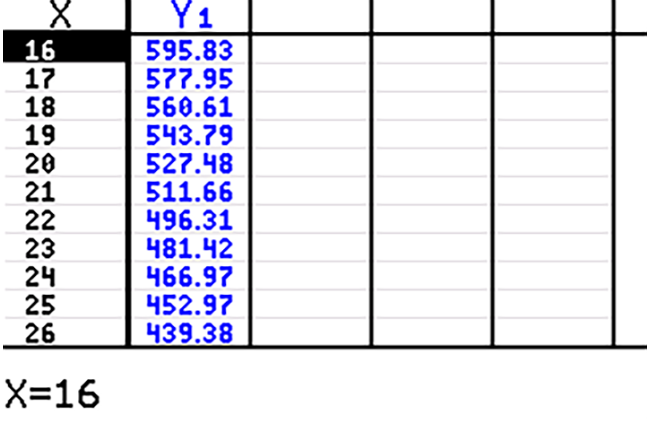
Maak een tabel van deze functie, bijvoorbeeld met een spreadsheet of een grafische rekenmachine.
Op
`t=21`
is de waarde van
`A`
ongeveer
`512`
. En op
`t=22`
is de waarde van
`A`
ongeveer
`496`
. Dus bij
`t=22`
komt het aantal abonnementen voor het eerst
onder de
`500000`
. De krant raakt in 2032 in de problemen.
Bekijk de tabel in Voorbeeld 2.
Controleer dat de groeifactor per jaar inderdaad ongeveer `0,97` is.
Welke formule vind je voor het aantal abonnementen `A(t)` als je `t=0` neemt in 2017?
Laat zien dat de krant in 2032 in de problemen raakt.
Neem de tabel over en vul in.
| procentuele toename per jaar | `13` | `text(-)6` | `0,3` | ||||
| groeifactor per jaar | `1,15` | `0,98` | `3,95` | `0,01` |