Exponenten en machten > Exponentiële functiesVoorbeeld 1
In een stedelijk gebied liggen twee steden: stad A met
`750000`
inwoners en stad B met
`620000`
inwoners op 1 januari 2013. In stad A groeide het aantal inwoners de laatste jaren gemiddeld met
`2,5`
% per jaar, in stad B was dat
`3,1`
%.
Na hoeveel jaren heeft stad B meer inwoners dan stad A als deze ontwikkeling zo doorgaat?
De groeifactor van het aantal inwoners van A is `1,025` . Die van het aantal inwoners van B is `1,031` . Dat B harder groeit dan A is duidelijk. Als `A` het aantal inwoners van stad A voorstelt, en `B` dat van stad B, beide in duizendtallen, en `t` de tijd in jaren vanaf 1 januari 2013, dan zijn beide groeifuncties:
-
`A(t)=750 *1,025^t` ;
-
`B(t)=620 *1,031^t` .
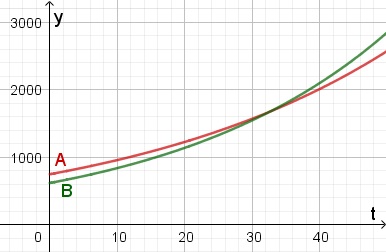
De bijbehorende grafieken maak je met GeoGebra of een grafische rekenmachine en je bepaalt het snijpunt. Neem voor het venster `[0, 50] xx [0, 3000]` . Ga na dat je `t~~32,6138` vindt.
Conclusie: `33` jaar na 1 januari 2013 heeft stad B meer inwoners dan stad A als je ervan uitgaat dat er steeds op 1 januari wordt geteld.
Bekijk Voorbeeld 1.
Waaraan zie je dat B harder groeit dan A?
Ga na dat je voor het snijpunt van beide grafieken inderdaad `t=32,6138 ...` vindt.
Een derde stad C is op 1 januari 2013 kleiner dan zowel A als B, maar deze stad groeit met `8,3` % per jaar. Op 1 januari 2021 heeft C evenveel inwoners als B. Wanneer is C even groot als A?
In een meer is op een bepaald moment een schadelijke stof aanwezig met een concentratie van `40` mg/L. De concentratie vervalt exponentieel met `20` % per dag.
Leg uit waarom de groeifactor per dag `0,80` is.
Breng de grafiek van `C(t)` in beeld.
Bereken in twee decimalen nauwkeurig vanaf welk tijdstip de concentratie niet meer meetbaar is, dus `C(t) lt 1` .