Exponenten en machten > Exponentiële functiesVoorbeeld 3
Gegeven is de functie
`g`
met voorschrift
`g(x)=16 -2 *2^ (text(-) x+1)`
.
Laat zien hoe deze functie door transformatie ontstaat uit een standaardfunctie van de vorm
`y=g^x`
en los algebraïsch op:
`g(x) gt 0`
.
Eerst herleiden:
`g(x)=16 -2 *2^ (text(-) x+1)`
`g(x) =text(-)2 *2^(text(-)x) *2^1+16`
`g(x)=text(-)4 * (2^(text(-)1))^x+16`
, dus
`g(x)=text(-)4 *0,5^x+16`
.
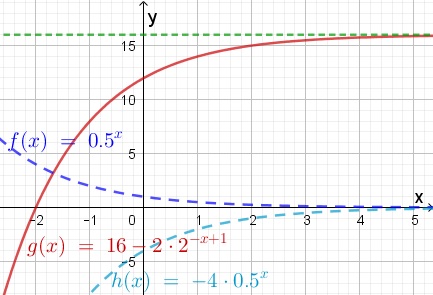
De grafiek van de functie `g(x)=text(-)4 *0,5^x+16` ontstaat door transformatie van `y=0,5^x` in twee stappen.
-
vermenigvuldiging in de `y` -richting met `text(-)4` ;
-
translatie in de `y` -richting met `16` eenheden.
Voor het oplossen van `g(x)=0` is het oorspronkelijke voorschrift handiger: `16 -2 *2^ (text(-)x+1) =0` geeft: `16 =2 *2^ (text(-) x+1)` . Nu is `16 =2^4` en `2 =2^1` , dus: `2^4=2^ (text(-) x+2)` . Dit betekent dat: `4 =text(-) x+2` , zodat `x=text(-)2` .
Uit de grafiek volgt de oplossing van de ongelijkheid: `x gt text(-)2`
De grafiek van de functie `f(x)=2 *2^ (x+1) -1` kun je door transformatie uit de grafiek van de functie `y=2^x` laten ontstaan.
Je kunt dit doen door drie transformaties toe te passen. Welke drie? Schrijf ze in de juiste volgorde op.
Je kunt ook eerst het functievoorschrift van `f` herleiden tot `f(x)=4 *2^x-1` .
Laat zien hoe deze herleiding gaat.
Beschrijf nu hoe je door transformatie in twee stappen de grafiek van `f` kunt laten ontstaan uit die van `g` .
Het punt `(0 , 1)` op de grafiek van `g` wordt na de transformaties een punt op de grafiek van `f` . Geef de coördinaten van dit punt.
Los op `f(x) gt 0` op.
Je hebt allerlei technieken geleerd om vergelijkingen algebraïsch op te lossen. Je kunt bijvoorbeeld de rekenregels voor machten gebruiken. Bekijk dit voorbeeld van een algebraïsche oplossing.
| `4 * (1/2) ^ (1 -x) -2 sqrt(2 )` | `=` | `6 sqrt(2 )` | |
| `4 * (1/2) ^ (1 -x)` | `=` | `8 sqrt(2 )` | |
| `(1/2) ^ (1 -x)` | `=` | `2 sqrt(2 )` | |
| `(2^(text(-)1)) ^ (1 -x)` | `=` | `2^(1 1/2)` | |
| `2^(x-1)` | `=` | `2^(1 1/2)` | |
| `x-1` | `=` | `1 1/2` | |
| `x` | `=` | `2 1/2` |
Los algebraïsch op: `4 *3^x+6 =330`
Los algebraïsch op: `sqrt(2 )* (1/3)^(x+1) =27 sqrt(6 )`
Los op:
`40 * (1/3) ^x+100 ge 110`
.
Vereenvoudig de bijbehorende vergelijking eerst zover mogelijk en gebruik daarna GeoGebra of een grafische rekenmachine. Geef je antwoord in twee decimalen nauwkeurig.