Antwoorden van de opgaven
Twee.
Een ruit.
Als je `/_BAD` een sterretje geeft, moet de hoek er tegenover ook een sterretje krijgen. De twee hoeken die er tegenaan liggen krijgen een rondje. Zie figuur.

Zie figuur.

Zie figuur, vergelijk ook de figuren van enkele medeleerlingen.

`/_ A_3` .
`/_ B_1`
`/_ B_1`
`/_ B_4`
`/_ A_1 ~~ 40^@` . De halve hoek is dus `20^@` en de twee hoeken om de deellijn zijn ook `20^@` .
`/_A_2 ~~ 140^@` . De halve hoek is dus `70^@` .
`90^@` , want `20^@ + 70^@ = 90^@` . Je hoeft dus niet te meten.
`(80^@)/2 = 40^@` . Zie figuur bij b.
Zie figuur.

Gebruik `(56^@)/2 = 28^@` en `(124^@)/2 = 62^@` om de deellijnen te tekenen. Zie figuur.

`28^@ + 62^@ = 90^@`
Alle hoeken rond punt
`C`
zijn recht, dus
`90^@`
.
En vanwege Z-hoeken is
`/_B_6 = /_C`
.
`/_ B_3 = /_B_6` (X-hoeken).
Dat zijn X-hoeken (overstaande hoeken).
`k` en `n` zijn halve lijnen die niet precies in elkaars verlengde liggen.
`k` en `q` zijn evenwijdig en dus zijn dit gelijke F-hoeken.
Omdat `p` en `l` geen evenwijdige lijnen zijn.
`/_ C_3 = /_ C_1` (overstaande hoeken) en `/_ C_1 = /_ A_1` (gelijke F-hoeken).
Als het goed is krijg je dezelfde figuur als in het voorbeeld.
`/_ C = 60^@` (opmeten), dus de halve hoek is `30^@` . En zo verder.
De drie deellijnen gaan door één punt.
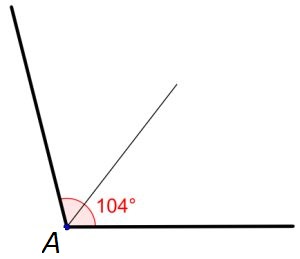
`/_A ~~ 104^@` , dus de deellijn moet een hoek maken van `52^@` .
`/_B ~~ 52^@` , dus de deellijn moet een hoek maken van `26^@` .
`/_C ~~ 230^@` , dus de deellijn moet een hoek maken van `115^@` .
Laat je tekeningen door iemand anders nameten. Vraag bij twijfel je leraar of je het goed hebt gedaan.
Verdeel `/_A = 104^@` in `/_A_1 = 52^@` en `/_A_2 = 52^@` .
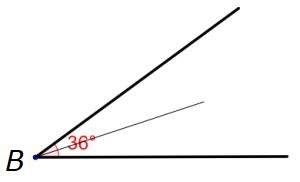
Verdeel `/_B = 36^@` in `/_B_1 = 18^@` en `/_B_2 = 18^@` .
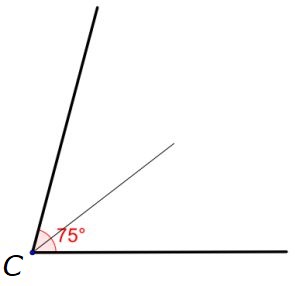
Verdeel `/_C = 75^@` in `/_C_1 = 37,5^@` en `/_C_2 = 37,5^@` .
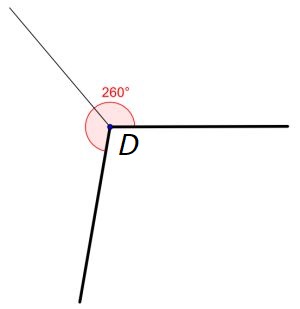
Verdeel `/_D = 260^@` in `/_D_1 = 130^@` en `/_D_2 = 130^@` .
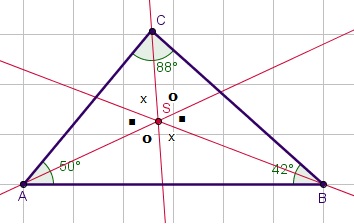
De figuur (zie bij b) is gemaakt in GeoGebra. Dan hoef je zelf de hoeken niet te meten, je kunt de grootte opvragen in dit programma.
`/_A_3 = /_A_1`
(X-hoeken)
`/_B_1 = /_A_1`
(F-hoeken)
`/_B_4 = /_A_1`
(Z-hoeken).
De lijnen `q` en `s` lopen niet evenwijdig.
`/_B_2 = /_B_5` (X-hoeken).
Teken eerst
`AB = 6`
cm met daarop
`/_A = 50^@`
.
Meet
`AD = 4`
cm af.
Teken een lijn door
`D`
en evenwijdig aan
`AB`
.
Teken een lijn door
`B`
en evenwijdig aan
`BC`
.
Teken nu punt
`D`
en het parallellogram.
Verleng de lijnstukken van het parallellogram naar alle kanten en je krijgt situaties van evenwijdige lijnen gesneden door een derde lijn en dus allemaal F-hoeken, Z-hoeken en X-hoeken. Zet in alle hoeken die gelijk zijn aan `/_BAD` een rondje.
Je ziet dan dat `/_BCD = /_BAD` .
Zie figuur.

Zoek de benodigde gegevens op een teken een bovenaanzicht van het strafschopgebied met de doel er in. Zet de keeper op de deellijn van de hoek tussen de benen van de punt van het strafschopgebied naar elk van beide doelpalen.

`/_C_3` (X-hoeken), `/_A_2` (F-hoeken) en `/_A_5` (Z-hoeken).
`/_A_3` en `/_A_6` .