Samenvatten
In dit onderwerp heb je je bezig gehouden met statistische gegevens en situaties waarin het toeval een rol speelt. Je hebt je vaardigheden op het gebied van het samenvatten van data met behulp van centrummaten en spreidingsmaten herhaald. En je hebt een eerste indruk gekregen van statistisch onderzoek, ook met grotere verzamelingen gegevens. Werken met een computerprogramma is daarbij onontbeerlijk.
De onderstaande opgaven zijn bedoeld om overzicht over het onderwerp "Statistiek" te krijgen. Dit betreft de onderdelen 1, 2, 3 en 4 van dit onderwerp. Het is nuttig om er een eigen samenvatting bij te maken. De opgaven hieronder zijn bedoeld om je daarbij te helpen.
Je kunt ook deze spiekbriefjes gebruiken.
Je doet met een groepje leerlingen een statistisch onderzoek. Jullie willen weten hoeveel procent van de Nederlanders regelmatig twittert. Waarom zijn de volgende steekproeven niet representatief?
Jullie vragen uit elke klas van jullie eigen school vier willekeurige leerlingen of ze wel of niet minstens één keer per week twitteren.
Jullie gaan in een winkelcentrum staan en vragen daar de bezoekers die voorbijkomen of ze wel of niet minstens één keer per week twitteren.
Het bedenken van een manier om een goede steekproef te maken is nog niet zo eenvoudig. Beschrijf een aantal voorwaarden waaraan een representatieve steekproef in dit geval moet voldoen.
Je moet diverse leeftijdscategorieën in de juiste verhouding hebben. Je moet zowel mensen die handig zijn met de pc in de steekproef hebben als mensen die weinig met een pc van doen hebben. Je moet hoger opgeleiden en lager opgeleiden in de juiste verhouding hebben. En zo zijn er nog wel meer voorwaarden te bedenken.
Open het Excel-bestand Sportprestaties. Je vindt er gegevens van leerlingen in de leeftijdscategorie 11-12 jaar.
De kolom
"Sprint (sec)"
geeft de tijden die deze leerlingen hebben gelopen over een sprint van m.
Maak een frequentietabel van deze tijden voor de jongens en de meisjes afzonderlijk. Maak eerst een klassenindeling met als eerste klasse .
Teken bijbehorende staafdiagrammen van de relatieve frequenties. Waarom neem je relatieve frequenties? Kun je een conclusie trekken?
Sla je resultaten op.
Open het in de vorige opgave opgeslagen Excel-bestand Sportprestaties. Je hebt van de jongens en de meisjes afzonderlijk frequentietabellen gemaakt. Veel verschil tussen beide bijpassende staafdiagrammen is er niet.
Je kunt nog bekijken wat de centrummaten en de spreidingsmaten opleveren. Die bepaal je het liefst van de ruwe data, niet uit de frequentietabellen.
Bepaal het gemiddelde en de mediaan van zowel de sprintgegevens van de meisjes als die van de jongens.
Bereken de spreidingsbreedtes en de kwartielen. Bereken de kwartielafstanden.
Teken bijpassende boxplots in één figuur. Zijn er nu conclusies te trekken?
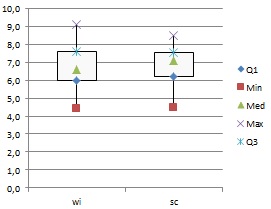
Je ziet hier boxplots van de jaarresultaten van klas 3G voor wiskunde en science.
Waaraan zie je dat het hier om de niet afgeronde jaarcijfers gaat?
Voor welk vak werd het hoogste cijfer gehaald? Welk cijfer was dat?
Wat kun je zeggen over deze resultaten als je beide vakken vergelijkt?
% van de cijfers voor science ligt tussen de en de . Is dat percentage bij wiskunde groter of kleiner?
In deze frequentietabel zie je de resultaten van tellingen van het aantal eieren dat dagelijks in een hok vol kippen werd geraapt.
| aantal eieren | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| frequentie | 1 | 2 | 3 | 6 | 12 | 15 | 27 | 35 | 23 | 12 |
Op grond van deze tabel kun je de kans schatten dat je op een bepaalde dag eieren in dit kippenhok kunt rapen.
Hoeveel dagen werd er geteld om de tabel te kunnen maken? Hoeveel eieren werden op die dagen in totaal geraapt?
Hoe groot is de kans dat op een willekeurige dag eieren worden geraapt?
Hoe groot is de kans dat op een willekeurige dag minstens eieren worden geraapt?

Voor het slot van een kluis wordt een vijfcijferige code gebruikt. Alle cijfers , , t/m zijn toegestaan.
Hoeveel verschillende codes kun je zo maken? Gebruik een wegendiagram om dit duidelijk te maken.
Hoeveel verschillende codes zijn er waarvan alle cijfers verschillend zijn?
Je bent de code die je hebt ingesteld vergeten. Je weet alleen de eerste twee cijfers nog.
Hoe groot is de kans dat je de goede code kiest?
Opeens bedenk je dat de cijfers van je code allemaal verschillend zijn.
Hoe groot is nu de kans dat je de goede code kiest?
Je gooit met twee dobbelstenen.
Hoe groot is de kans dat er samen meer dan ogen boven komen te liggen?