Antwoorden van de opgaven
Ja, natuurlijk. De stijging wordt soms sterker, maar neemt soms ook af. Dit geldt ook voor de daling.
Zo ongeveer midden tussen eb en vloed in.
Die houdt dan op en gaat over in daling. Op het moment zelf is de stijging dus `0` m/s.
`T` neemt toe.
`T` neemt steeds sterker toe.
Afnemende daling: steeds minder sterke daling, `T` daalt steeds minder snel.
Bij
`t=4`
is de dagtemperatuur
`7`
°C en bij
`t=8`
is het
`10`
°C.
De temperatuur stijgt met
`3`
°C.
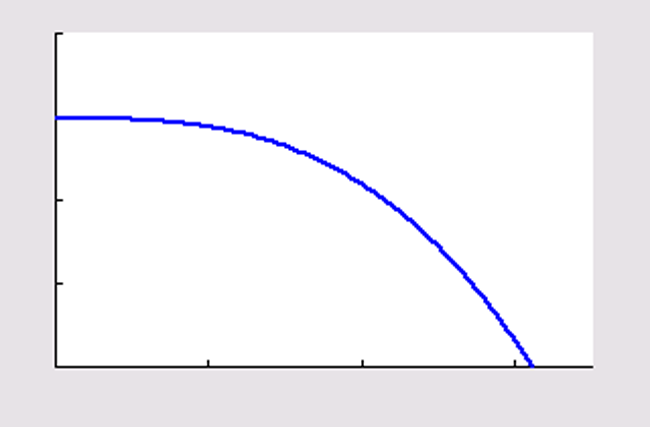
toenemende daling |
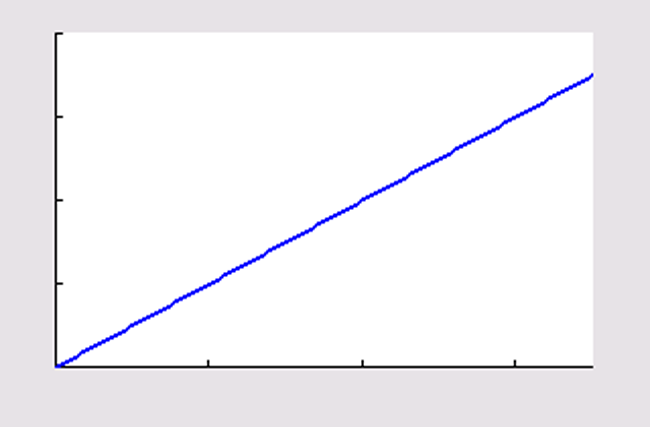
constante stijging |
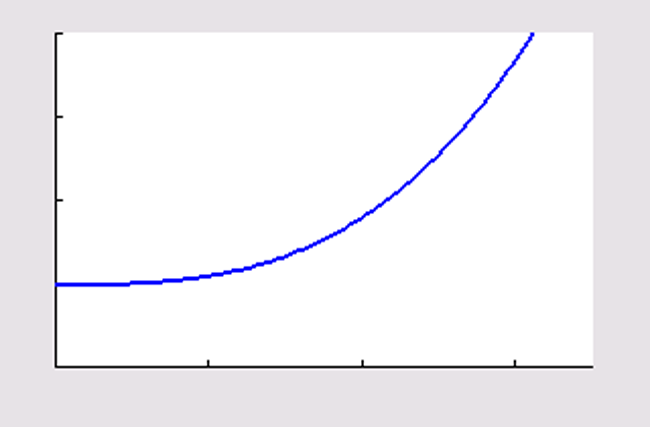
toenemende stijging |
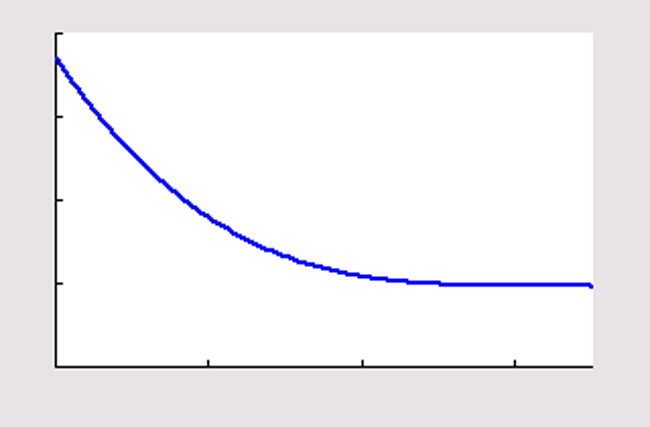
afnemende daling |
afnemende stijging |
constante daling |
`0,5` (voor `x=2` )
Op welk interval is er sprake van toenemende daling?
`⟨ text(-)0,5 ; 0,75 ⟩`
`⟨ 0,75 ; 2 ⟩`
`〈 2 ; 4,2 〉` , of `〈 2 , → 〉` als de grafiek naar beide zijden op dezelfde manier door loopt.
`⟨ text(-)2,5 ; text(-)0,5 ⟩` en `⟨ 2; 4,2 ⟩` , of `⟨ ← ; text(-)0,5 ⟩` en `⟨ 2 , → ⟩` als de grafiek naar beide zijden op dezelfde manier door loopt.
Voer in Y1=-X^2+6X met venster `text(-)2 le x le 6` bij `text(-)10 le y le 10` .
De grafiek is stijgend voor de top bij `x=3` , dus op het interval `⟨ ← , 3 ⟩` .
Om welke soort stijging gaat het bij a?
toenemende stijging
afnemende stijging
constante stijging
Is er in de grafiek sprake van toenemende of afnemende daling?
toenemende daling
afnemende daling
Deze grafiek heeft een top. Hoort daarbij een minimum of een maximum?
een minimum van `9`
een maximum van `9`
De grafiek heeft een minimum bij `x = 5` .

Je ziet bijna altijd maar een deel van de grafiek en je weet dus nooit zeker of je alle toppen van de grafiek wel ziet.
`(: ← , text(-)1 :)`
: afnemende stijging
`(: text(-)1, 0 :)`
: toenemende daling
`(: 0, 1 :)`
: afnemende daling
`(: 1 , → :)`
: toenemende stijging
max.
`y ( text(-)1 ) ≈ 4`
en min.
`y ( 1 ) ≈ text(-)4`
.
In
`( 0, 0 )`
is de daling het snelst, de helling het steilst.
`⟨ ← , text(-)2 ⟩`
: afnemende daling
`⟨ text(-)2, 0 ⟩`
: toenemende stijging
`⟨ 0, 2 ⟩`
: afnemende stijging
`⟨ 2 , → ⟩`
: toenemende daling
max.
`y ( 2 ) = 16`
en min.
`y ( -2 ) = -16`
.
In
`( 0, 0 )`
is de stijging het snelst, de helling het steilst.
Voer in:
`y_1=0,5x^4-4x^2+8`
.
Venster bijvoorbeeld:
`text(-)5<x<5`
en
`text(-)5<y<10`
.
Maximum is
`8`
voor
`x=0`
.
Er is twee keer een minimum van
`0`
voor
`x=text(-)2`
en
`x=2`
.
twee intervallen
Afnemende stijging en toenemende daling.
Op
`langle 0, 200 rangle`
: afnemende stijging.
Op
`langle 200, 400 rangle`
: toenemende daling.
`q=100, W=300` en `q=200, W=400` .
De winst neemt met
`400-300=100`
toe.
Dit komt overeen met
`100*100=10000`
, ofwel € 10000,00.
Het maximum ligt bij
`q=200`
,
`W=400`
.
Dit komt overeen met
`400*100=40000`
, ofwel € 40000,00.
Maximumtemperatuur om 14:30 uur, de grafiek gaat daar over van stijgend in dalend.

`q=100`
geeft
`W=290`
.
De winst is € 290000,00.
Plot de grafiek.
Voer in:
`y_1=text(-)0,02x^2+5x-10`
.
Venster bijvoorbeeld:
`0<x<250`
en
`0<y<350`
.
De top zit op
`q=125`
.
`langle 0, 125 rangle` : afnemende stijging.
`langle 125, rarr rangle` : toenemende daling.
`q=125`
geeft
`W=302,5`
.
De maximale winst is € 302500,00.
Na `60` seconden, daar zit een knik in de grafiek en vanaf dat punt is de daalsnelheid constant. De knik duidt erop dat er iets veranderde op dat moment en de constante en afgenomen daling duidt erop dat hij zijn parachute heeft geopend en dus geleidelijk naar beneden komt.
De grafiek daalt steeds steiler, de valsnelheid wordt dus steeds groter.
De grafiek is een rechte lijn. De valsnelheid is dan `10` m/s.
Zijn achttiende levensjaar; `27` cm.
Vanaf 13 tot 21 jaar.
Vanaf 18 tot 21 jaar.
Vanaf 21 jaar tot ...?
Vanaf 13 tot 15 jaar en vanaf 21 jaar tot ...? Dan is de grafiek min of meer recht.
`⟨ text(-)2,0 ⟩` en `⟨ 2 , → ⟩`
Eén interval.
Maximum van `8` en een minimum van `0` .