Data verwerken > Verdelingen typerenVoorbeeld 1
Gebruik weer de dataset Gegevens 154 havo 4-leerlingen.
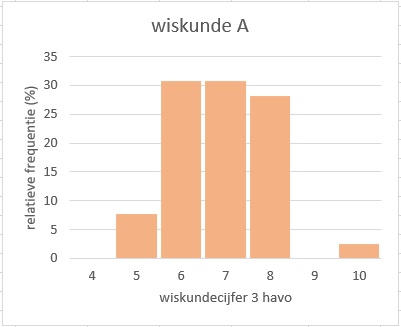
Je wilt nagaan of leerlingen die wiskunde B kiezen, beter waren in wiskunde in de onderbouw dan leerlingen die wiskunde A kiezen. Daartoe bekijk je de variabele cijfers (het eindcijfer voor wiskunde in havo 3) voor elk van deze deelgroepen.
|
|
|
Het linker diagram lijkt redelijk symmetrisch met als top het cijfer `8` . De mediaan van deze gegevens is `8` en het gemiddelde is `7,7` . Het rechter diagram is in het midden meer gelijkmatig en er is geen echte top. De mediaan van deze gegevens is `7` en het gemiddelde `6,9` . Het cijfer `10` wijkt behoorlijk veel af van de andere cijfers, maar is nog net geen uitschieter.
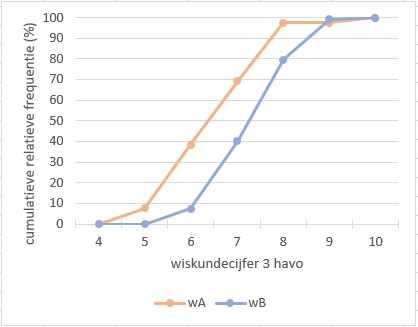
Bekijk de somfrequentiepolygonen van beide verdelingen.
Je ziet dat de wiskunde B-leerlingen stelselmatig hogere cijfers hebben (op de uitschieter na). Ongeveer `40` % van de A-leerlingen had bijvoorbeeld een wiskundecijfer `6` of lager, tegen nog geen `10` % van de B-leerlingen.
Bekijk Voorbeeld 1. Alle percentages zijn gehele getallen.
Waarom zijn geen van beide verdelingen scheef?
Reken de gemiddelden en de medianen van beide verdelingen na.
De somfrequenties zijn uitgezet tegen de gehele cijfers 5, 6, 7, 8, 9, 10. Is dat hier correct?
Hoeveel procent van de leerlingen met wiskunde A heeft een cijfer 7 of lager? En hoeveel procent van de leerlingen met wiskunde B heeft zo’n cijfer? Kun je nu iets zeggen over het aantal leerlingen met een 7 of lager?
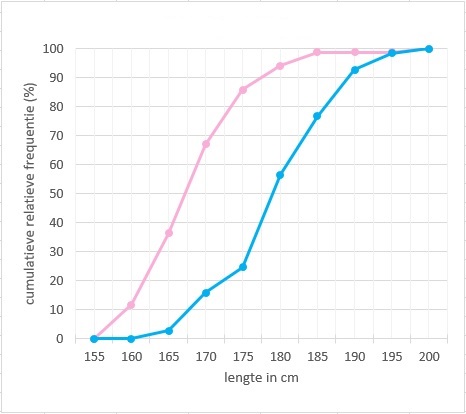
Bekijk de frequenties (in procenten) van de lengtes van de `154` meisjes en jongens in een brugklas.
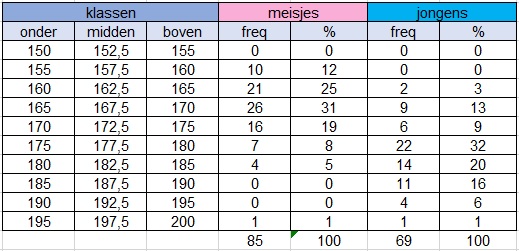
Welke somfrequentiepolygoon hoort bij de meisjes en welke bij de jongens? Licht je antwoord toe.
Welke conclusie kun je uit dit cumulatief frequentiepolygoon trekken?