Antwoorden van de opgaven
Doen, bepaal met behulp van Excel of de GR het gemiddelde en de standaardafwijking.
Nee.
Een manier is om van alle leeftijdsklasse de cumulatieve frequentiepolygoon op normaal-waarschijnlijkheidspapier te tekenen en een verticale lijn door `78,5` te tekenen en vandaar verder te rekenen.
Een andere manier is om van elke leeftijdsklasse de gewone frequentiepolygoon te tekenen; allen in hetzelfde assenstelsel en ook met die verticale lijn door `78,5` kg.
Je kunt ook iedere leeftijdsklasse standaardiseren: hoe je dat doet, leer je in deze paragraaf.
Als het goed is krijg je een rechte lijn die bij op % zit.
Ja, zie figuur.
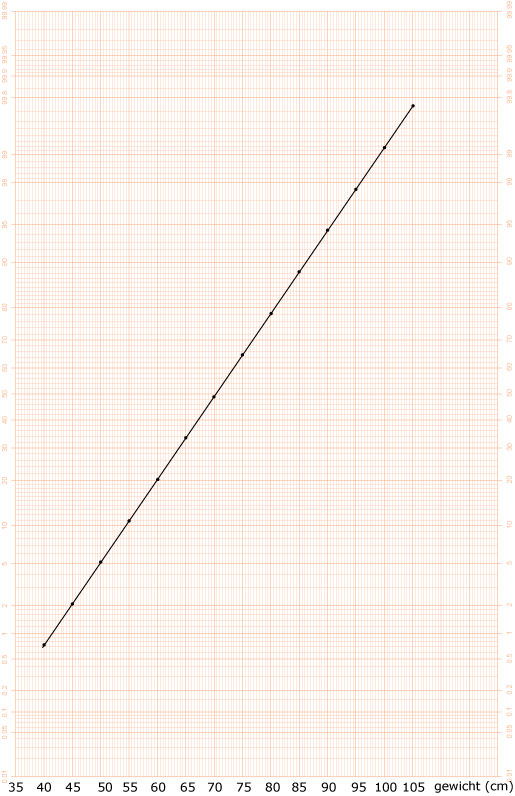
Bij % kun je aflezen en bij kun je aflezen (vuistregels).
Zie tabel.

Zie figuur.
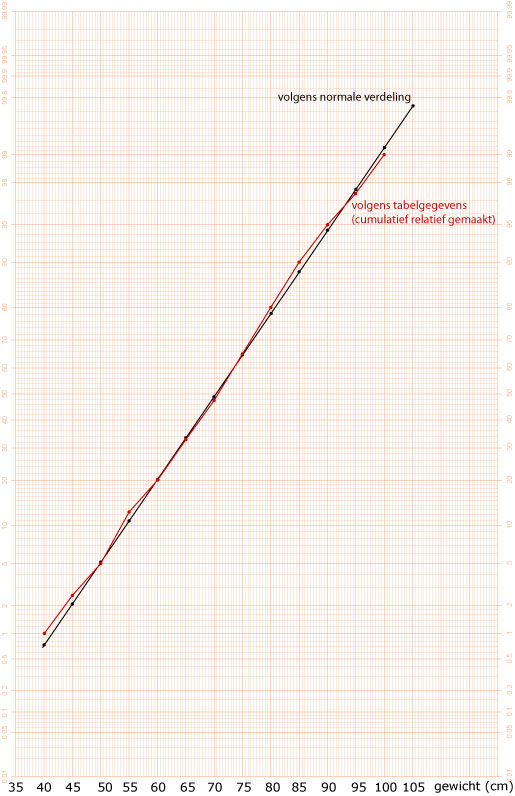
De verschillen zijn niet erg groot. Je moet de bovengrenzen van de klassen gebruiken omdat het om "kleiner of gelijk" kansen gaat.
Ja.
Gebruik de statistiekfuncties van de grafische rekenmachine of bereken het gemiddelde en de standaardafwijking handmatig. Denk daarbij aan de klassenmiddens.
Gebruik: `μ = bar M = 13,20` hoort bij `50` % en `μ + σ = 13,20 + 0,10 = 13,30` hoort bij `84` %.

De cumulatieve percentages zijn: `0,1` ; `2,2` ; `15,8` ; `49,9` ; `83,9` ; `97,5` ; `99,5` en `99,6` .
Teken de punten bij deze percentages: plaats de punten recht boven de rechterklassengrenzen (eerste punt `(12,9; 0,1)` , dan `(13,0; 2,2)` enzovoort).
Dat klopt, behalve aan het eind (wat wel vaker het geval zal zijn).
Gebruik de gegevens van machine 1 en werk met Excel.
In de kop van de tabel betekent c.r.f. cumulatieve relatieve frequenties.
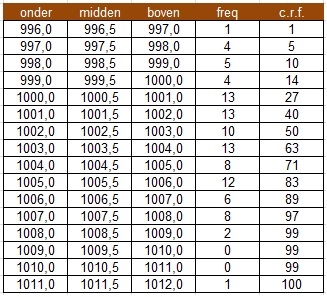
Laat Excel dit voor je doen.
Dit geeft: `μ≈1003,1` en `σ≈3,0` gram.
Gebruik de bovengrens van elke klasse!

Dit klopt, er kan redelijk goed een rechte lijn door de punten worden getekend.
Dit hangt van de getekende rechte lijn af. Hier is sprake van een schatting en dit kan per persoon wat afwijken.
-
Lees `μ` af bij `50` %.
-
Lees `μ+σ` af bij `84` % en bereken daarmee `σ` .
De waarden zouden ongeveer gelijk moeten zijn aan die bij b.
Aflezen bij
`90`
% geeft ongeveer (afhankelijk van de rechte lijn)
`1007`
gram.
De zwaarste pakken wegen
`1007`
gram of meer.
Lees af: bij `18` cm hoort `30` %, dus `30` % van de sneeuwdagen valt er `18` cm of minder sneeuw.
Dit betekent dat op de rest van de sneeuwdagen meer dan `18` cm sneeuw valt. Dat komt overeen met `70` %.
`S` , de hoeveelheid sneeuw die valt op een dag dat het sneeuwt, is normaal verdeeld omdat de grafiek van de cumulatieve relatieve frequentieverdeling van `S` op normaal-waarschijnlijkheidspapier een rechte lijn is.
Lees de gemiddelde hoeveelheid sneeuw af bij `50` %: ongeveer `23` cm sneeuw per dag dat het sneeuwt.
Lees bijvoorbeeld de hoeveelheid sneeuw af bij `16` %: dat is `14` cm. Het verschil tussen `14` en `23` cm is de standaardafwijking: `9` cm sneeuw.
Bijvoorbeeld bij schoenmaat
`5,5`
krijg je
`z= (5,5 - 11)/(1,5) ~~ text(-)3,7`
.
De andere schoenmaten gaan net zo.
| schoenmaat | `z` -waarde |
| `5,5` | `text(-)3,7` |
| `6,5` | `text(-)3` |
| `9,5` | `text(-)1` |
| `10,25` | `text(-)0,5` |
| `11` | `0` |
| `12,5` | `1` |
| `13,25` | `1,5` |
| `13,5` | `1,7` |
Over schoenmaat `11` kun je direct concluderen dat de `z` -waarde gelijk is aan `0` . Deze schoenmaat is de gemiddelde waarde: de `z` -waarde is de hoeveelheid standaardafwijkingen die een schoenmaat afwijkt van de gemiddelde schoenmaat.
De `z` -waarden van de schoenmaten `6,5` en `12,5` (en eventueel ook van `13,25` ) bepaal je zonder de formule voor de `z` -waarde omdat de standaardafwijking van de schoenmaten `1,5` is. Je berekent dat `9,5` precies één standaardafwijking kleiner is dan de gemiddelde schoenmaat `11` . De `z` -waarde van schoenmaat `9,5` is gelijk aan `text(-)1` . Bepaal zo ook de `z` -waarden van schoenmaten `6,5` , `12,5` en eventueel `13,25` .
Mannen met een schoenmaat die groter is dan `13,5` hebben een schoenmaat die bijna twee keer of meer keer de standaardafwijking (de `z` -waarde) groter is dan de gemiddelde schoenmaat.
Grofweg `95` % van de mannen heeft een schoenmaat tussen `μ-2σ` en `μ+2 σ` .
Dat betekent dat grofweg `5` % van de mannen een schoenmaat heeft die ofwel kleiner is dan `μ-2 σ ` ( `2,5` %) ofwel groter dan `μ+2σ` ( `2,5` %).
In dit geval heeft meer dan `2,5` % van de Amerikaanse mannen een grotere schoenmaat dan maat `13,5` .
`z=3` betekent een schoenmaat van `11 + 3*1,5 = 15,5` .
Voer alle lijsten op de grafische rekenmachine in en laat voor beide groepen de statistische berekeningen uitvoeren.
Mannen: `bar x ≈ 128,5` mm Hg en `σ≈12,6` mm Hg.
Vrouwen: `bar x ≈ 131,7` mm Hg en `σ≈13,7` mm Hg.
De genoemde bloeddrukwaarden zijn de klassenmiddens.
De klassenbreedte is `5` en de eerste klasse is `102,5\- < 107,5` .
Maak eerst een tabel met cumulatieve relatieve frequenties (in procenten).
Zet de frequenties uit tegen de rechter klassengrenzen.
De punten liggen niet op een rechte lijn. Dit betekent dat de bloeddruk van deze mannen niet normaal is verdeeld.
Iedereen zal net een andere rechte lijn tekenen en zo uitkomen op een eigen gemiddelde en standaardafwijking. Alle lijnen zullen behoorlijk afwijken van de berekende waarden.
Bekijk de frequentieverdeling in de frequentietabel: de hoogste frequenties zitten bovenin en niet in het midden. Dit betekent dat deze frequentie links scheef is verdeeld en niet normaal is (klokvormig) verdeeld.
Je kunt ook normaal-waarschijnlijkheidspapier gebruiken om dit aan te tonen.
Frequentietabel:
| hoogte (meter) | `< 1,5` | `1,5 - 3` | `3 - 5` | `5 - 7` | `7 - 10` | `10 - 15` | `> 15` |
| aantal waarnemingen | `24` | `26` | `51` | `72` | `122` | `92` | `13` |
| cumulatieve waarnemingen | `24` | `50` | `101` | `173` | `295` | `387` | `400` |
| cum. rel. waarnemingen (%) | `6` | `12 1/2` | `25 1/4` | `43 1/4` | `73 3/4` | `96 3/4` | `100` |
Zet de punten uit op normaal-waarschijnlijkheidspapier (bij de rechterklassengrenzen).
De punten liggen grofweg op een rechte lijn: de hoogte is daarom bij benadering normaal verdeeld.
Het gemiddelde is af te lezen bij `50` %: `mu~~7,6` meter.
Bij `84` % hoort `~~11,6` meter, dus de standaardafwijking is `σ ~~ (11,6 - 7,6) = 4,0` meter.
(naar: examen vwo wiskunde A in 2002, eerste tijdvak)
`μ≈43,6` en `σ≈2,7` cm.
Maak eerst de cumulatieve relatieve frequentieverdeling in procenten. Zet deze waarden uit tegen de rechter klassengrenzen.
Doen.
Ja, de kniehoogte van deze `5001` vrouwen is redelijk goed normaal verdeeld.
Tussen `41,3` en `45,9` cm. Dus `a≈2,3` cm.
`46,4` cm of meer.