Antwoorden van de opgaven
Zie tabel.
| `g` | `text(P)(G≤g)` | kans in % |
| `40` | `0,0073` | `0,7` |
| `45` | `0,0209` | `2,1` |
| `50` | `0,0514` | `5,1` |
| `55` | `0,1101` | `11,0` |
| `60` | `0,2058` | `20,6` |
| `65` | `0,3388` | `33,9` |
| `70` | `0,4958` | `49,6` |
| `75` | `0,6534` | `65,3` |
| `80` | `0,7881` | `78,8` |
| `85` | `0,8859` | `88,6` |
| `90` | `0,9463` | `94,6` |
| `95` | `0,9781` | `97,8` |
| `100` | `0,9923` | `99,2` |
| `105` | `0,9976` | `99,8` |
Zie figuur.
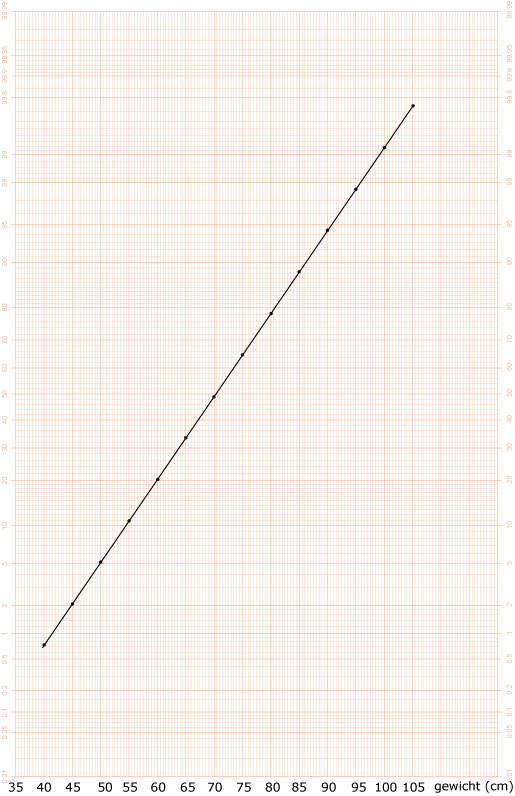
Ja, zie figuur bij b.
Bij
`50`
% lees je de waarde van
`mu`
af, ongeveer
`70`
.
Bij
`84%`
lees je de waarde van
`mu + sigma`
af (vuistregels), ongeveer
`82,5`
.
`sigma=82,5-70=12,5`
.
Zie tabel.
| gewicht | frequentie | cum. freq. | cum.rel.freq. |
| `35- <40` | `10` | `10` | `1` |
| `40- <45` | `15` | `25` | `2,5` |
| `45- <50` | `25` | `50` | `5` |
| `50- <55` | `75` | `125` | `12,5` |
| `55- <60` | `75` | `200` | `20` |
| `60- <65` | `125` | `325` | `32,5` |
| `65- <70` | `150` | `475` | `47,5` |
| `70- <75` | `175` | `650` | `65` |
| `75- <80` | `150` | `800` | `80` |
| `80- <85` | `100` | `900` | `90` |
| `85- <90` | `50` | `950` | `95` |
| `90- <95` | `25` | `975` | `97,5` |
| `95- <100` | `15` | `990` | `99` |
| `100- <105` | `10` | `1000` | `100` |
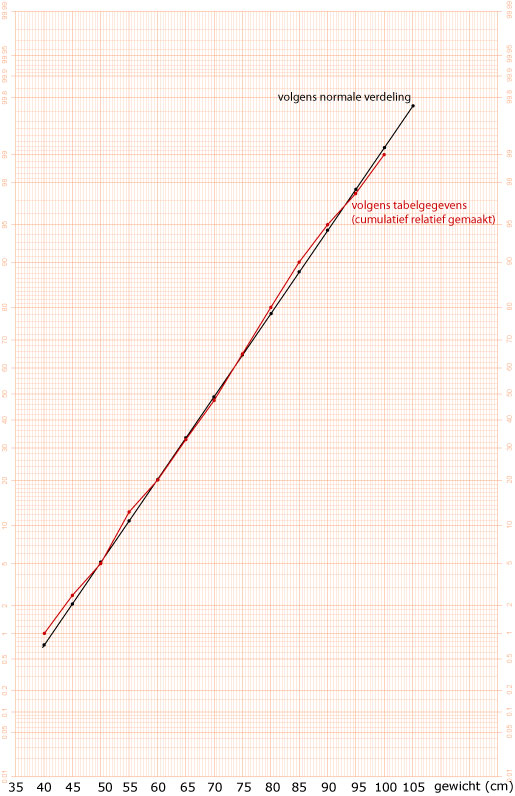
Je moet de bovengrenzen van de klassen gebruiken omdat het om "kleiner-of-gelijk-kansen" gaat.
De verschillen zijn niet erg groot.
Ja, want de punten (kansen) liggen allemaal nagenoeg op een rechte lijn.
Voer in: `text(normalcdf)(1000, 10^(99), 970, sqrt(650))` .
`text(P)(T>1000|mu=970text( en )sigma=sqrt(650))~~0,1197`
Voer in: `text(normalcdf)(30, 10^(99), 0, sqrt(1250))` .
`text(P)(V>30|mu=0text( en )sigma=sqrt(1250))~~0,1981`
Voer in: `text(normalcdf)(text(-)10^(99), 950, 970, sqrt(650))` .
`text(P)(T<950|mu=970text( en )sigma=sqrt(650))~~0,2165`
`text(P)(T>g)=0,1` geeft `text(P)(T<g)=1-0,1=0,9` .
Voer in: `text(invNorm)(0,9; 970; sqrt(650))` .
Je vindt `g~~1002,67` , dus minimaal ongeveer `1003` gram.
`mu(2F)=mu(F)+mu(F)=2·850=1700` gram en de standaardafwijking is `sigma(2F)=sqrt((sigma(F))^2+(sigma(F))^2)=sqrt(25^2+25^2)=sqrt(1250)~~35,36` gram.
Dit kan natuurlijk ook met de `sqrt(n)` -wet, want het gaat hier om twee dezelfde stochasten.
`text(P)(T<1650|mu=1700text( en )sigma=sqrt(1250))~~0,0786`
Voer de klassenmiddens en de relatieve frequenties in je grafische rekenmachine in en bereken het gemiddelde en de standaardafwijking.
| `g` | `text(P)(M≤g)` | percentage |
| `12,9` | `0,013` | `1,3` |
| `13,0` | `0,023` | `2,3` |
| `13,1` | `0,159` | `15,9` |
| `13,2` | `0,5` | `50` |
| `13,3` | `0,841` | `84,1` |
| `13,4` | `0,977` | `97,7` |
| `13,5` | `0,999` | `99,9` |
| `13,6` | `1` | `100` |
Zie figuur bij d.
Maak eerst deze tabel:
| diameter | percentage | cum.perc. |
| `12,8- <12,9` | `0,1` | `0,1` |
| `12,9- <13,0` | `2,1` | `2,2` |
| `13,0- <13,1` | `13,6` | `15,8` |
| `13,1- <13,2` | `34,1` | `49,9` |
| `13,2- <13,3` | `34,0` | `83,9` |
| `13,3- <13,4` | `13,7` | `97,6` |
| `13,4- <13,5` | `2,2` | `99,8` |
| `13,5- <13,6` | `0,2` | `100` |
Zie figuur.

Dat betekent dat de verdeling van de diameters van de schroeven ongeveer een normale verdeling is.
Voer de klassenmiddens en de frequenties in je grafische rekenmachine in.
Je vindt dan:
`mu~~225,4`
en
`sigma~~10,8`
.
Zie tabel.
| lengte (cm) | percentage | cum.perc. |
| `190- <195` | `0,3` | `0,3` |
| `195- <200` | `0,9` | `1,4` |
| `200- <205` | `1,6` | `3,0` |
| `205- <210` | `6,8` | `9,8` |
| `210- <215` | `5,1` | `14,9` |
| `215- <220` | `21,1` | `36,0` |
| `220- <225` | `13,5` | `49,5` |
| `225- <230` | `16,5` | `66,0` |
| `230- <235` | `19,5` | `85,5` |
| `235- <240` | `4,0` | `89,5` |
| `240- <245` | `7,3` | `96,8` |
| `245- <250` | `2,5` | `99,3` |
| `250- <255` | `0,7` | `100` |
Teken zo goed mogelijk een rechte lijn door de punten.
Ja, de punten liggen vrijwel op een rechte lijn, dus er is sprake van een normale verdeling.
Lees het gemiddelde af bij `50` % en gemiddelde plus standaardafwijking bij `84` %.
Laat Excel dit voor je doen. Of voer de gegevens in de GR in.
Dit geeft: `μ≈1003,1` en `σ≈3,0` gram.
In de kop van de tabel betekent c.r.f. cumulatieve relatieve frequenties.
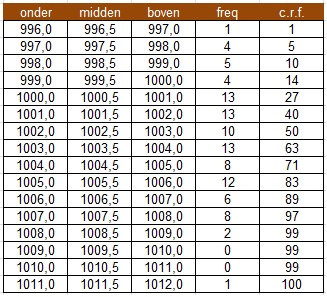
Zie figuur.

Dit klopt, er kan redelijk goed een rechte lijn door de punten worden getekend.
Dit hangt van de getekende rechte lijn af. Hier is sprake van een schatting en dit kan per persoon wat afwijken.
Aflezen bij `90` % geeft ongeveer (afhankelijk van de rechte lijn) `1007` gram. De zwaarste pakken wegen `1007` gram of meer.
Voer in: `text(normalcdf)(0; 0,25; 0,15; sqrt(0,02))` .
`text(P)(0≤V≤0,25|mu=0,15 text( en )sigma=sqrt(0,02))≈0,62`
.
`62`
% past wel, dus
`38`
% past niet.
Ongeveer `30` % van de bouten is te dik.
Het gewicht van `100` bouten en moeren bedraagt gemiddeld `1230` gram met een standaardafwijking van `sqrt(13)~~3,6` gram.
Ongeveer `8,3` % van de dozen.
`V=15B-D`
`mu(V) = mu(15B)-mu(D)= 15·7-83= 22`
cm.
`sigma(V)=sqrt(15·(sigma(B))^2+(sigma(D))^2) = sqrt(15·1,3^2 +0,9^2)=sqrt(26,16)`
cm.
Het past als
`V < 0`
.
`text(P)(V<0|mu=3text( en )sigma=sqrt(26,16))~~ 0,3479`
Aflezen bij `660` uren. Dat is ongeveer `89` %. Dus ongeveer `100-89=11` % van de dagproductie gaat langer mee dan `660` uren.
Het gemiddelde
`mu`
aflezen bij
`50`
% geeft
`mu = 600`
uren.
`mu+sigma`
aflezen bij
`84`
% geeft
`651`
uren. Dus
`sigma=651-600=51`
uren.
Aflezen bij `97,5` % geeft `696` uren. Dus deze batterijen gaan minstens `696` uren mee.
`K` is het gewicht van het kleine pak suiker en `G` van het grote pak.
Laat `T=K+G` de somstochast zijn met `mu(T)=mu(K)+mu(G)=1002+503-1505` gram en `sigma(T)=sqrt((sigma(K))^2+(sigma(G))^2)=sqrt(6,3^2+3,9^2)=sqrt(54,9)` gram.
`text(P)(T>1500|mu=1505text( en )sigma=sqrt(54,9))~~0,7501`
Voer de gegevens in de GR in.
Mannen:
`mu ~~ 128,5`
en
`sigma ~~ 12,6`
.
Vrouwen:
`mu ~~ 131,7`
en
`sigma ~~ 13,7`
.
De genoemde bloeddrukwaarden zijn de klassenmiddens.
Klassenbreedte `5` en eerste klasse `102,5 - < 107,5` .
Breid de tabel uit met relatieve frequenties en cumulatieve relatieve frequenties.
De punten (cum. rel. freq.) uitgezet tegen rechter klassengrenzen liggen niet echt op een rechte lijn.

Bij de lijn hoort een gemiddelde (bij
`50`
%) van ongeveer
`131,5`
cm en de standaardafwijking
`12`
cm.
Wijkt toch wel behoorlijk af.
Nee, de bloeddruk van de vrouwen is ook niet normaal verdeeld. Beide verdelingen zijn behoorlijk scheef.
`V = text(aankomsttijd Merel) - text(aankomsttijd Eefje)`
, ofwel
`V=M-E`
.
`mu(V) = mu(M)-mu(E)=11:18- 11:16= 2`
min.
`sigma(V) = sqrt((sigma(M))^2+(sigma(E))^2)=sqrt(5^2+7^2)=sqrt(74)~~8,60`
minuten.
Merel komt eerder dan Eefje in Arnhem aan als
`V < 0`
.
`text(P)(V<0|mu=2text( en )sigma=sqrt(74))~~0,4081`
Als
`26`
% harder rijdt dan
`126`
km/u dan rijdt dus
`74`
% langzamer.
De lijn op normaal-waarschijnlijkheidspapier gaat door de punten
`(105, 12)`
en
`(126, 74)`
.
Dat geeft `mu ~~ 118,8` km/u en `sigma ~~ 130,2-118,8=11,4` km/u.
Noem
`V`
het verschil van springer A en springer B, ofwel
`V=A-B`
.
`mu(V) = mu(A)-mu(B)=8,60 - 8,50 = 0,10`
`sigma(V) = sqrt(0,1^2 + 0,2^2) = sqrt(0,05)~~0,224`
Als A verder springt dan B dan moet gelden
`V > 0`
.
`text(P)(V > 0|mu=0,10text( en )sigma=sqrt(0,05))=0,6726...` .
De kans dat verspringer A beide keren verder springt dan verspringer B is `0,6726...^2~~0,452` .
`88`
% heeft minder dan
`280`
, dus de lijn moet door punt
`P(280, 88)`
gaan.
Teken een willekeurige lijn met een standaardafwijking van
`17`
cm (tussen
`50`
% en
`84`
% een breedte
`17`
).
Teken dan door
`P`
een lijn evenwijdig aan deze lijn.
Aflezen bij
`240`
cm geeft ongeveer
`11`
%.
De gemiddelde lengte is `162` cm en de standaardafwijking is `6,5` cm.
Ja, de lichaamslengte van deze vrouwen is redelijk goed normaal verdeeld. Want de punten liggen nagenoeg op een rechte lijn.
Je moet aflezen bij `2,5` % en `97,5` %.
Ongeveer tussen `149` en `175` cm. Dus `a ~~ 13` cm.
Dat betekent dat je bij `84` % moet aflezen.
Ongeveer `169` cm of groter.
`mu ~~ 43,6` en `sigma ~~ 2,7` cm.
Je krijgt een redelijk rechte lijn.
Ja, de kniehoogte van deze `5001` vrouwen is redelijk goed normaal verdeeld.
Lees `mu` af bij `50` % en `mu+sigma` bij `84` %.
Tussen `41,3` en `45,9` cm. Dus `a ~~ 2,3` cm.
`46,4` cm of meer.
Laat `T=A+B` de somstochast zijn, met `mu(T)=mu(A)+mu(B)=80+55=135` cm en `sigma(T)=sqrt((sigma(A))^2+(sigma(B))^2)=sqrt(4^2+3^2)=5` cm.
`text(P)(T>140|mu=135text( en )sigma=5)~~0,1587`
Laat `V=A-B` de verschilstochast zijn, met `mu(V)=mu(A)-mu(B)=80-55=25` cm en `sigma(V)=sqrt((sigma(A))^2+(sigma(B))^2)=sqrt(4^2+3^2)=5` cm.
`text(P)(V<30|mu=135text( en )sigma=5)~~0,8413`
Laat `T=A+2B` de somstochast zijn, met `mu(T)=mu(A)+mu(2B)=80+2·55=190` cm en `sigma(T)=sqrt((sigma(A))^2+2·(sigma(B))^2)=sqrt(4^2+2·3^2)=sqrt(34)~~5,83` cm.
`text(P)(T<185|mu=1190text( en )sigma=sqrt(34))~~0,1956`
Op normaal-waarschijnlijkheidspapier krijg je nagenoeg een rechte lijn.
`mu = 180,7` cm en de standaardafwijking is ongeveer `sigma=187,5 - 180,7 = 6,8` cm.
Ongeveer `91` %.
`70` % van de dagen waarop het sneeuwde viel er meer dan `18` cm sneeuw.
`S` , de hoeveelheid sneeuw die valt op een dag dat het sneeuwt, is normaal verdeeld omdat de grafiek van de cumulatieve relatieve frequentieverdeling van `S` op normaal-waarschijnlijkheidspapier een rechte lijn is.
De gemiddelde hoeveelheid per dag dat het sneeuwt, is ongeveer `23` cm sneeuw en de standaardafwijking is ongeveer `9` cm.
In ongeveer `24` % van de gevallen.
Ongeveer `1003,2` mL zijn.