In de wiskunde versta je onder een afstand altijd de lengte van de kortste verbinding. Bij twee punten op een kaart is dat hemelsbreed gemeten, dus de lengte van het lijnstuk tussen beide punten.

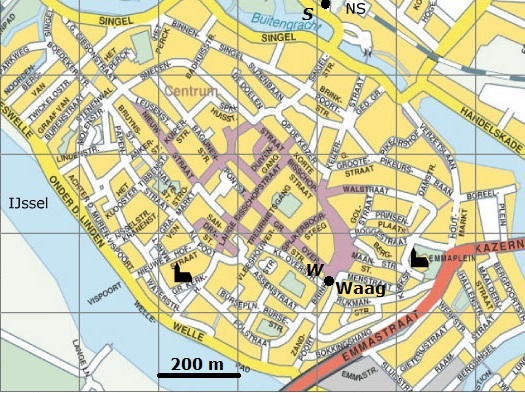
Op deze kaart zie je bij het NS-station een punt ( `S` ) en bij de Waag een punt ( `W` ). De afstand tussen deze twee punten is de lengte van het lijnstuk `SW` . Iedere andere verbinding tussen beide punten is langer.

De kortste afstand tussen de Waag en de Emmastraat is de lengte van het kortste lijnstuk dat je vanuit `W` naar een punt op die straat kunt trekken. Is die straat een rechte lijn `l` dan teken je dit lijnstuk loodrecht op lijn `l` . De lengte van het lijnstuk is dan de afstand van punt `W` tot lijn `l` . Het lijnstuk ligt op de loodlijn door punt `W` op lijn `l` .

Om de werkelijke afstand te berekenen moet je rekening houden met de schaal van de kaart. Die schaal wordt bepaald door het schaallijntje. Op deze kaart is elke cm ongeveer `200` m, dus `200 xx 100 = 20000` cm. De schaal is daarom `1 : 20000` . Elke gemeten cm is in werkelijkheid `20000` keer zo groot.