Hoeken

Hoeken > Hoeken meten

Overzicht

123456Hoeken meten

Antwoorden van de opgaven

Opgave V1

Je kunt er `0` en `360` bij zetten.

Niet binnen de getallen op deze windroos waarbij je één keer de hele cirkel doorloopt.

`90` graden.

Noordoosten: `45` graden; noordnoordoost: `22,5` graden.

Zuid: `180` graden; zuidzuidoost: `157,5` graden.

West: `270` graden; westnoordwest: `292,5` graden.

Opgave 1

Er zijn meerdere goede antwoorden op deze vraag. Bijvoorbeeld:

De geodriehoek heeft twee schaalverdelingen, zowel rechtsom (met de wijzers van de klok mee) als linksom.
De schaalverdelingen op de geodriehoek beginnen niet bovenaan.
De kompasroos loopt helemaal rond van `0^@` tot en met `360^@` , de geodriehoek niet.

`90^@`

Opgave 2

Een gestrekte hoek is `180^@` .

Elk deel is een rechte hoek. Een rechte hoek is `90^@` .

`45^@`

Pas ze op de gradenboog van een tweede geodriehoek, met de punt op de `0` in het midden van de langste zijde.

Een geodriehoek heeft twee hoeken van `45^@` en één hoek van `90^@` .

Opgave 3

Tussen `0@` en `90@` .

`/_ B` is

groter dan een halve rechte hoek

kleiner dan een halve rechte hoek

Ongeveer `70@` .

Ongeveer `130@` .

Opgave 4

`/_ A ~~ 45^@`
`/_ B ~~ 100^@`
`/_ C ~~ 45^@`
`/_ D ~~ 130^@`
`/_ E = 90^@`
`/_ F ~~ 100^@`

Opgave 5

Neem de tijd voor oefening, zeker zolang je nog fouten maakt. Door het hokje aan te vinken, krijg je het juiste antwoord te zien.

Opgave 6

Bepaal eerst of de hoek scherp of stomp is, je kunt dan vooraf het aantal graden schatten!

`/_A ~~ 35^@`

Opgave 7

Je meet dan niet de overstrekte hoek, maar juist de andere, kleinere, hoek tussen beide benen. De gemeten hoek is samen met de overstrekte hoek altijd `360^@` . Dus trek je je antwoord van de `360` af en zo vind je het juiste aantal graden voor de overstrekte hoek.

Opgave 8

`/_ A ~~ 50^@`

`/_ A ~~ 54^@`

`/_ B ~~ 64^@` en `/_ C ~~ 62^@` .

Opgave 9

Welke hoek is stomp?

`/_ A`

`/_ B`

`/_ C`

Omdat dan twee zijden geen snijpunt hebben en er dus geen driehoek kan ontstaan.

`/_ C ~~ 127^@`

`/_A ~~ 22^@` en `/_B~~31^@` .

`/_A + /_B + /_C = 127^@ + 22^@ + 31^@ = 180^@`

Opgave 10

`/_ A ~~ 115^@`
`/_ B ~~ 80^@`
`/_ C = 180^@`
`/_ D ~~ 250^@`
`/_ E ~~ 60^@`
`/_ F ~~ 100^@`

Opgave 11

`/_ A ~~ 66^@`
`/_ B ~~ 73^@`
`/_ C ~~ 41^@`

`180^@`

`/_ K ~~ 30^@`
`/_ L ~~ 245^@`
`/_ M ~~ 30^@`
`/_ N ~~ 55^@`

`30^@ + 245^@ + 30^@ + 55^@ = 360^@`

Opgave 12

De twee hoeken aan de onderkant van de plattegrond zijn ongeveer `67^@` en `113^@` . De twee hoeken rechtsboven zijn ongeveer `80^@` en `100^@` .

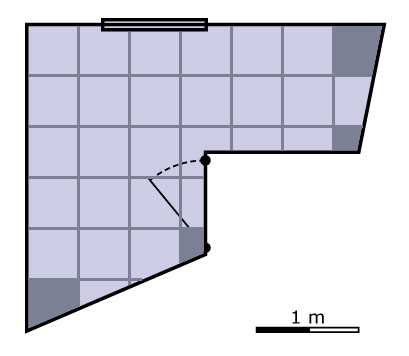
Ze heeft in totaal `19` hele tegels nodig en `12` delen van tegels.

Opgave 13

`/_ BSC ~~ 80^@`

`/_ ASD`

`/_ ABC ~~ 113^@`
`/_ BCD ~~ 67^@`
`/_CDA ~~ 78^@`
`/_DAB ~~ 102^@`
De hoeken van de vierhoek zijn samen `360^@` .

Opgave 14

De toren van Pisa maakt een hoek van ongeveer `85^@` met de grond.

Opgave 15

Ongeveer `37^@` .

Opgave 16Hoekmeter

Hoekmeter

Bijvoorbeeld:

De zwaaihaak die in de bouw wordt gebruikt.
De sextant die vroeger in de scheepvaart werd gebruikt.
De theodoliet die door landmeters wordt gebruikt.

Opgave 17Vliegerij

Vliegerij

Als je er van uit gaat dat er eerst richting Deventer wordt gevlogen, dan krijg je ongeveer deze koersvectoren:
`(92^@ | 10,8)` , `(189^@ | 4,2)` , `(261^@ | 7,1)` en `(330^@ | 6,3)` .

Doen.

Opgave 18

`/_ A ~~ 160^@` , `/_ B ~~ 45^@` , `/_ C ~~ 100^@` , `/_ D ~~ 25^@` , `/_ E ~~ 245^@` en `/_ F ~~ 60^@` .

Opgave 19

`/_A` en `/_D` .

`/_B` en `/_C` .

`/_E` . Deze hoek kun je meten met een geodriehoek door de andere kant van de hoek te meten en die waarde van `360^@` af te trekken.

`/_A ~~ 37^@` ; `/_B ~~ 119^@` ; `/_C ~~ 123^@` ; `/_D ~~ 41^@` ; `/_E ~~ 220^@` .

`540^@`

verder | terug