Antwoorden van de opgaven
Zie figuur.
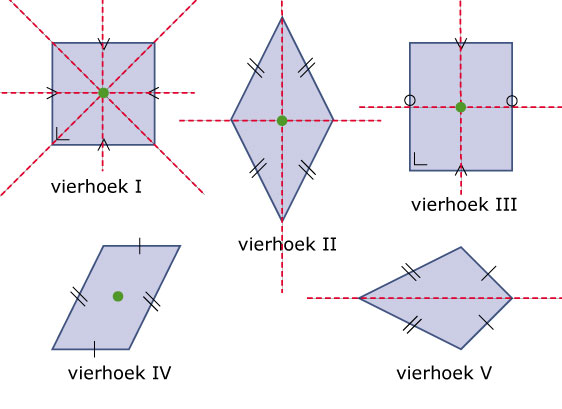
De vierhoeken I, II, III en IV. Zie figuur bij a.
De vierhoeken I (), II (), III () en IV ().
Geef ze in de figuur op het werkblad aan. De hoeken onder en boven zijn gelijk en de hoeken links en rechts zijn gelijk.
Geef ze in de figuur op het werkblad aan. De hoeken linksonder en rechtsboven zijn gelijk en de hoeken rechtsonder en linksboven zijn ook gelijk.
Geef ze in de figuur op het werkblad aan. De hoeken onder en boven zijn gelijk.
Vierhoek I: vierkant.
Vierhoek II: ruit.
Vierhoek III: rechthoek.
Vierhoek IV: parallellogram.
Vierhoek V: vlieger.
Het trapezium.
Deze uitspraak klopt. Het omgekeerde niet: een trapezium hoeft geen parallellogram te zijn.
Deze uitspraak klopt. Het omgekeerde niet: een parallellogram hoeft geen ruit te zijn want de zijden hoeven niet alle vier even lang te zijn.
Ja, dat is een vierkant.
Doen. In de voorbeelden kom je deze vierhoeken en hun eigenschappen nog tegen. Vergelijk je eigen antwoord met wat je in elk van de voorbeelden aantreft.
Alleen en kun je vrij bewegen. Als die twee punten eenmaal hun plek hebben dan kan alleen nog loodrecht op bewegen, want de hoek bij moet recht blijven. Als dan zijn plek heeft, dan ligt de plaats van punt vast.
Doordat de rechthoek twee symmetrieassen heeft door de middens van de zijden en door het snijpunt van de diagonalen zijn alle vier de lijnstukken , , en even lang.
Door punt te verschuiven tot alle vier de zijden even lang zijn.
Twee, bijvoorbeeld de lengte en de breedte.
Of de lengte van beide diagonalen en de hoek er tussen. Of...
Alleen en kun je vrij bewegen. Als die twee punten eenmaal hun plek hebben dan kan alleen nog over de symmetrieas bewegen. Punt kun je nu nog bewegen, maar dan beweegt symmetrisch mee.
In de figuur ligt diagonaal op de symmetrieas en de punten en elkaars spiegeldbeeld. Dus is de middelloodlijn van .
Door punt te verschuiven tot alle vier de zijden even lang zijn.
Je kunt er inderdaad ook een vierkant van maken, want dat is een ruit met rechte hoeken.
Drie, bijvoorbeeld de lengtes van twee opeenvolgende ongelijke zijden en de hoek tussen die twee zijden.
Twee, bijvoorbeeld de lengte van de zijden en de hoek tussen twee zijden.
Als de lijnstukken en vast liggen, dan ligt ook vast als spiegelbeeld van bij puntspiegeling ten opzichte van het midden van .
Doen.
Een ruit, een rechthoek en een vierkant.
Drie, bijvoorbeeld de lengtes van twee opeenvolgende ongelijke zijden en de hoek tussen die twee zijden.
Vier, bijvoorbeeld de lengtes van drie zijden en een hoek tussen twee zijden. (Bedenk nu maar eens hoe je het trapezium dan kunt tekenen. Het is leuk om meerdere manieren te bekijken waarop je een trtapezium kunt tekenen. Je zult zien dat je altijd minstens vier gegevens nodig hebt.)
Vierhoek I: ruit, de andere hoeken zijn , en .
Vierhoek II: parallellogram, de andere hoeken zijn , en .
Vierhoek III: vlieger (pijlpuntvlieger), de andere hoeken zijn , en .
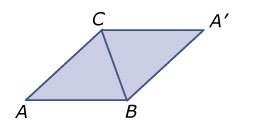
Zie figuur. Er ontstaat een ruit met twee hoeken van en twee hoeken van .
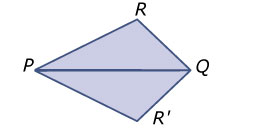
Zie figuur. Er ontstaat een vlieger met een hoeken van , een hoek van en twee hoeken van .
Je kunt op verschillende manieren een trapezium maken, bijvoorbeeld door te kiezen. En er zijn nog wel meer punten mogelijk.
Andere soorten bijzondere vierhoeken zijn echter niet mogelijk.
Een parallellogram.
Een strip die diagonaal wordt geplaatst. Je krijgt dan een driehoek met drie gegeven lengtes en die kan niet worden vervormd. Een driehoek is een starre figuur.
Twee hoeken van en nog een hoek van .
Linker figuur:
Bij het middelpunt zitten allemaal hoeken van . Vanwege de draaisymmetrie is elke punt een vlieger met een hoek van en een hoek van . De hoek met het rondje is dus .
Rechter figuur:
Bij het middelpunt zitten allemaal hoeken van . De ruiten tegen het middelpunt aan hebben dus hoeken van en . De ruiten die niet tegen het middelpunt aan zitten hebben grootste hoeken van en dus zijn de hoeken met de stip gelijk aan .
De blauwe vliegers hebben drie hoeken van en dus ook één van .
De oranje sterren hebben dus punten met een hoek van . De andere hoeken van de sterren zijn .
Begin met en spiegel dan punt in lijn om punt te krijgen.
Bereken eerst . Nu kun je de figuur gemakkelijk afmaken. Laat je antwoord controleren.
Bedenk dat ook . Nu kun je de figuur gemakkelijk afmaken. Laat je antwoord controleren.
en .
en .
en .
en .