Toepassen van formules

Toepassen van formules > Redeneren met formules

12345Redeneren met formules

Uitleg

Wanneer een zalmkwekerij een aantal zalmen in een vijver uitzet en de condities zijn in orde, dan zullen de vissen zich gaan vermenigvuldigen.
Het verband tussen de tijd $t$ in maanden nadat de eerste vissen in de vijver zijn uitgezet en het aantal vissen $a$ dat in de vijver leeft, wordt weergegeven met de formule:
$a = (3500)/(1 + 6*0,8^t)$

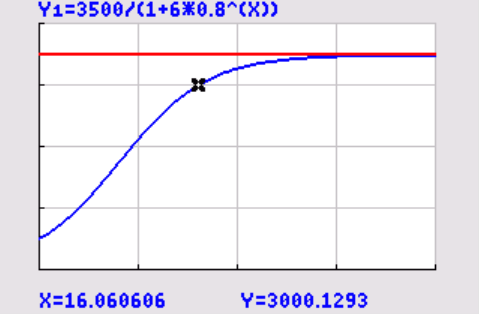
Bekijk de grafiek. Het aantal vissen in de vijver groeit eerst exponentieel, maar bereikt daarna een grenswaarde (het verzadigingsniveau). Dat komt doordat de vijver dan verzadigd is met vissen. Als er nog meer vissen bij zouden komen, dan zou er niet meer genoeg leefruimte zijn voor iedere vis. Wat die grenswaarde precies is, kun je afleiden uit de formule.

Wanneer je voor $t$ een heel grote waarde invult (bijvoorbeeld $1000000$ ), dan nadert $0,8^t$ naar $0$ .
Dit betekent dat $1 + 6*0,8^t$ naar $1$ nadert.
En dus nadert $3500/(1 + 6*0,8^t)$ naar $3500/1 = 3500$ .

De grenswaarde is dus $3500$ zalmen. De zalmkweker gaat voor het eerst zalmen vangen als er $3000$ vissen in de vijver zitten.
Om uit te zoeken na hoeveel maanden dat het geval is, moet je een vergelijking oplossen:

$3500/(1 + 6*0,8^t) = 3000$

Dit kun je schrijven als $1 + 6*0,8^t = 3500/3000 = 7/6$ en $0,8^t = 1/36$ zodat $t = \ ^(0,8)log(1/36) ~~ 16$ .

Na $16$ maanden wordt het aantal van $3000$ vissen in de vijver bereikt.

Opgave 1

Gebruik de gegevens uit Uitleg 1.

Bereken het aantal vissen dat volgens de eerste formule na tien maanden in de vijver zit.

Vul $t = 1000000$ in de formule in en laat daarmee zien dat de grenswaarde $3500$ is.

Welke ongelijkheid moet je oplossen als er maximaal $2600$ vissen in de vijver mogen zitten? Los deze ongelijkheid op.

Welke formule krijg je als de vissen zich twee keer zo snel gaan vermenigvuldigen? Neem $a_2$ voor het aantal vissen en $t$ voor de tijd in maanden.

Plot de grafieken van $a$ en de grafiek van $a_3$ .
Hoe wordt de grafiek van $a_2$ verkregen uit de grafiek van $a$ ?

Opgave 2

Beredeneer aan de hand van de functie of de bijbehorende grafiek stijgend of dalend is en welke grenswaarde de grafiek mogelijk benadert.

$f(x) = 720/(1+3*0,5^x)$

$g(x) = 500(3 - 0,75^x)$

$h(x) = (21 + 6*1,5^x)/250$

$i(x) = 55 - 33/(x + 1)$

Uitleg 2| Verkennen