Statistiek

Statistiek > Uitspraken doen

123456Uitspraken doen

Antwoorden van de opgaven

Opgave V1

Iemand's lengte is een natuurlijke maat (in tegenstelling tot iemand's gewicht, want dat is beïnvloedbaar). De waarden van dergelijke maten liggen vaak symmetrisch verdeeld aan weerszijden van de centrummaten. Die centrummaten zijn ook ongeveer hetzelfde: modus, mediaan en gemiddelde verschillen hier weinig. Verder is het vrijwel altijd zo dat grote afwijkingen van het gemiddelde zeldzamer worden naarmate een waarde verder van dat gemiddelde af zit.

Opgave 1

Zie de figuur.

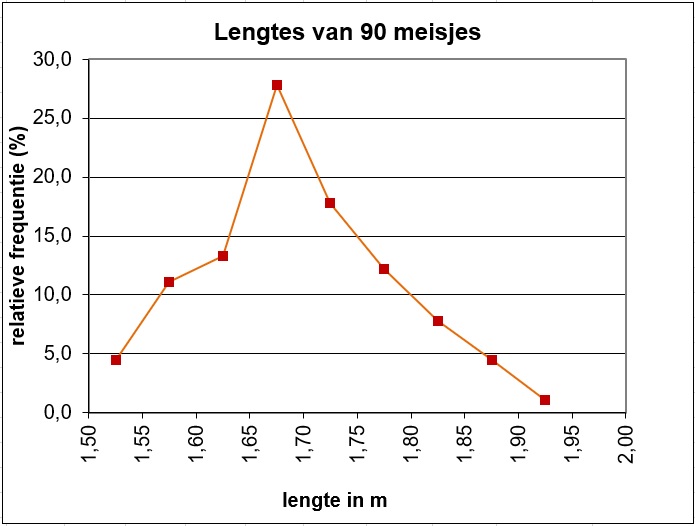
$bar(L) ~~169$ en $σ_L~~8,86$ .

Vuistregel 1: tussen $bar(x) - sigma_x$ en $bar(x) +sigma_x$ zit $68$ % van de waarnemingsgetallen.

$169 - 8,86 = 160,14$ cm.

$169 + 8,86 = 177,86$ cm.

Je kijkt naar de meisjes van $161$ cm tot en met $177$ cm. Dat zijn er $59$ van de $90$ .

$59/90*100 ~~ 65,6$ %.
Dat komt aardig dicht in de buurt van $68$ %.

Vuistregel 2: tussen $bar(x) - 2sigma_x$ en $bar(x) + 2sigma_x$ zit $95$ % van de waarnemingsgetallen.

$169 - 2*8,86 = 151,28$ cm.

$169 + 2*8,86 = 186,72$ cm.

Je kijkt naar de meisjes van $152$ cm tot en met $186$ cm. Dat zijn er $86$ van de $90$ .

$86/90*100~~95,6%$ . Dat klopt heel goed met $95%$ .

Opgave 2

$(100 - 68)/2 = 16$ % van de Nederlandse meisjes is langer dan $178$ cm.

$(100 - 95)/2 = 2,5$ % van de Nederlandse meisjes is korter dan $160$ cm.

Opgave 3

Relatief is het misschien wel lager, maar absoluut kan het evenveel of zelfs meer zijn.

Het aantal automobilisten dat geen alcohol heeft gedronken, is veel en veel hoger. Dus je moet het in verhouding zien tot het aantal automobilisten dat wel of geen alcohol heeft gedronken.

$20$ % witter dan wit. Waarmee wordt dat vergeleken?

Het slagingspercentage is vooral afhankelijk van de capaciteiten van de leerlingen die aan het examen deelnemen. Zorg je er als school voor dat alleen heel goede leerlingen in de examenklas komen, dan slagen waarschijnlijk veel leerlingen. Mogelijk komen veel leerlingen helemaal niet in de examenklas, maar verlaten de school vroegtijdig.

Opgave 4

$bar(L)~~180,8$ en $σ_L~~7,74$ . Je kunt de vuistregels het makkelijkst controleren door aflezen in een cumulatieve frequentiepolygoon. Daarin geef je $bar(L)+σ_L$ en $bar(L)-σ_L$ aan en kijk je of ongeveer $68$ % van de waarnemingen daarbinnen valt. Op dezelfde manier controleer je de andere vuistregel.

Opgave 5

Geef aan welke van de volgende beweringen waar zijn. Licht je antwoord toe.

Minimaal $25$ % van de batterijen gaat langer dan $3000$ uur mee.

Meer dan $50$ % van de batterijen heeft een levensduur van minder dan $2000$ uur.

De batterijen gaan gegarandeerd $1200$ uur mee.

Minstens $75$ % van de batterijen werkt nog na $1600$ uur.

Opgave 6

Geef aan welke uitspraken volgens de vuistregels waar zijn.

Ongeveer $95$ % van de pakken koffie heeft een gewicht tussen $246$ en $262$ gram.

Ongeveer $5$ % van de pakken koffie heeft een gewicht onder $246$ gram.

Ongeveer $16$ % van de pakken koffie heeft minder dan de beloofde $250$ gram inhoud.

Ongeveer $50$ % van de pakken koffie heeft een gewicht van $250$ gram.

Minimaal $75$ % van de pakken koffie heeft een gewicht van meer dan $250$ gram.

Opgave 7

Belgen spreken langzamer dan Nederlanders.

Het is niet eerlijk om voor het onderzoek alleen maar leraren en leraressen toe te laten tot de steekproef, deze groep mensen kan over het algemeen snel praten en is dus niet representatief voor de hele populatie.
Die "ene Antwerpse stotteraarster" is een uitschieter en kan wellicht beter buiten beschouwing worden gelaten. De steekproeven zijn veel te klein.

Vitalinea misleidt consument.

Er wordt al aangegeven dat het vreemd is dat we niets horen over de andere $20$ % van de deelnemers aan het onderzoek.
Bovendien wil het niet zeggen dat $80$ % van de deelnemers is afgevallen door Danone. Misschien zijn ze gezonder gaan leven?

Opgave 8

Duitsland, want er zijn veel meer Duitsers dan Nederlanders.

Het aantal inwoners van elk land.

$1019$ km per persoon.

België heeft met $327$ km bijna het dubbele van Italië ( $168$ ), maar de staaf is maar een klein beetje langer; de staaf van Groot-Brittannië moet meer dan drie keer zo lang zijn dan die van Spanje.

De hoogte van de fiets is dan de hoogte van de staaf. Maar de fietsen worden niet alleen hoger, maar ook breder en daarmee worden verschillen overdreven.

Opgave 9

Tussen $177,6 - 6,6 = 171,0$ cm en $177,6 + 6,6 = 184,2$ cm.

$27$ van de $36$ lengtes liggen tussen $171$ en $184,2$ cm: $27/36 * 100% = 75$ %. Dus geen $68$ %, zoals de eerste vuistregel zegt (gerekend met de niet afgeronde grenzen).

Reken je met de afgeronde grenzen ( $171$ en $184,5$ ), dan vind je dat er $24$ lengtes tussen deze waarden liggen. $24/36 * 100% = 66,7$ %. Dit percentage komt meer in de richting van $68$ %, de eerste vuistregel van de klokvormige frequentieverdeling.

Tussen $177,6 - 2*6,6 = 164,4$ cm en $177,6 + 2*6,6 = 190,8$ cm.

$34$ van de $36$ lengtes liggen tussen $164,4$ en $190,8$ cm ⇒ $34/36 * 100% = 94,4$ %. Dat ligt dicht tegen de $95$ % aan, zoals de tweede vuistregel zegt. Voldoet dus!

Opgave 10

$95$ cm. Het bezwaar is onnodig hoge kosten aan materiaal.

Vuistregel 1: tussen $bar(x) - sigma_x$ en $bar(x) + sigma_x$ zit $68$ % van de waarnemingsgetallen.

Dat betekent dat $34%$ tussen $bar(x)$ en $bar(x) + sigma_x$ zit . Je weet ook dat $50$ % van de mannen een lengte heeft van $bar(x)$ of minder.

$34$ % $+ 50$ % $= 84$ %.

De langste persoon van deze $84%$ heeft beenlengte $bar(x) +sigma_x = 80 + 5 = 85$ cm.

$bar(x) + sigma_x = 74 + 4 = 78$ cm.

Opgave 11

Voor iedereen geldt dat er $3$ % loon bijkomt. Alle lonen veranderen daardoor op een verschillende manier. De kwartielen, maximum en minimum worden alle vijf vermenigvuldigd zijn met $1,03$ . De boxplot krijgt een andere vorm.

Iedereen krijgt er precies € 200,00 bij: de boxplot behoudt daardoor zijn vorm, schuift alleen $200$ naar rechts.

De laagstbetaalde werknemers krijgen er niets bij.

Alleen de maximumwaarde komt $1800$ naar rechts te liggen.

Opgave 12

Geboortelengte: $68$ % van de pasgeborenen heeft een lengte tussen $48,0$ en $53,2$ cm en $95$ % heeft een lengte tussen $45,4$ en $55,8$ cm. De geboortelengte is gemiddeld ongeveer $50,6$ cm met een standaardafwijking van $2,6$ cm (gebruik hiervoor de klassenmiddens $44,5$ cm; $46,5$ cm; $48,5$ cm; ...; $56,5$ cm).

Geboortegewicht: $68$ % van de pasgeborenen heeft een gewicht tussen $2870$ en $4084$ gram en $95$ % heeft een gewicht tussen $2263$ en $4691$ gram. Het geboortegewicht is gemiddeld ongeveer $3477$ gram met een standaardafwijking van ongeveer $607$ gram (gebruik hiervoor de klassenmiddens $1250$ , $1750$ , $2250$ , ..., $4750$ ).

Opgave 13

De gemiddelde lengte is ongeveer $171$ cm. Mannen zijn gemiddeld $176$ cm met een standaardafwijking van $7$ cm en vrouwen gemiddeld $164$ cm met een standaardafwijking van $6$ cm. Mannen zijn gemiddeld langer dan vrouwen.

Dat klopt. De $50$ % langste mannen zijn minstens $176$ cm, de $84$ % kortste vrouwen zijn hoogstens $164 + 6 = 170$ cm.

Opgave 14

De hele grafiek is op "dalend roosterpapier" getekend.

Nee, dat is redelijk constant.

De lijn vrouwen van 65 jaar en ouder, daalt nooit of nauwelijks als je de percentages bekijkt.

Alle $29$ jaar $1$ % afname geeft $60 * 0,99^29 ≈ 45$ %, maar er was de eerste jaren meer afname; dus die $37$ % kan wel kloppen.

Opgave 15

Gebruik Excel. De gemiddelde lengte is ongeveer $162,1$ cm met standaardafwijking $6,5$ cm.

Zie figuur, gemaakt met Excel.

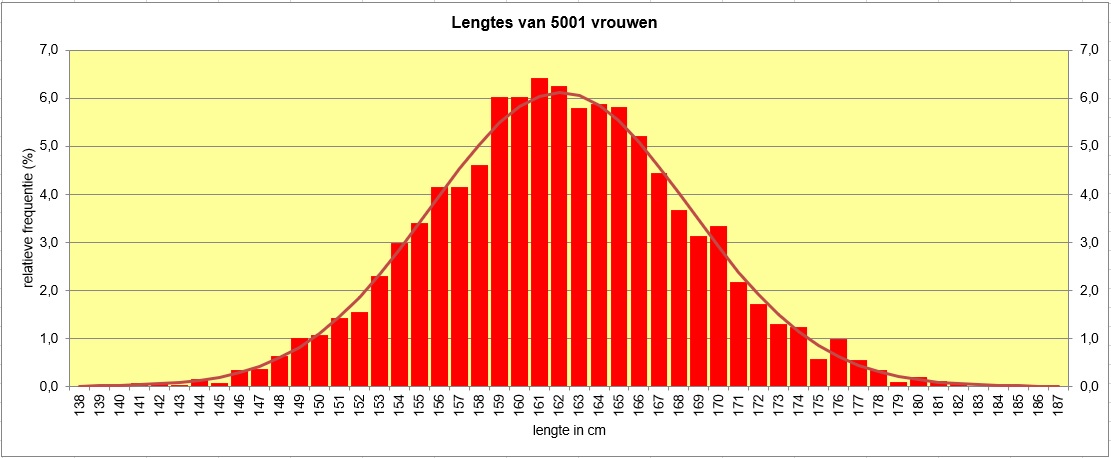
Het gaat om de lengtes van minder dan $162,1 - 6,5 = 155,6$ en meer dan $162,1 + 6,5 = 168,6$ cm.
Dat betreft $1575/5001*100~~31,5$ procent van de vrouwen.

Het gaat nu om de lengtes van minder dan $149,1$ en meer dan $175,1$ cm. Dat gaat om $263/5001~~5$ % van de vrouwen.

Ze komen aardig overeen met de vuistregels.

De gewichten vormen geen klokvormige frequentieverdeling.

Opgave 16

De $25$ % kortste mannen hebben lengtes vanaf $150$ tot $168,4$ cm.

$25$ % van $1064$ mannen is $266$ mannen. Klopt.

De verdeling is om twee redenen niet symmetrisch.

De afstand van $Q_1$ tot de mediaan is korter dan de afstand van de mediaan tot $Q_3$ .
De afstand van de linkergrens tot de mediaan is korter dan de afstand van mediaan tot de rechtergrens.

Opgave 17

De gemiddelde leeftijden zijn achtereenvolgens $39,2$ ; $40,5$ ; $42,35$ ; $45,85$ ; $48,1$ .

De standaarddeviaties zijn achtereenvolgens $9,7$ ; $8,8$ ; $8,4$ ; $8,3$ ; $9,3$ .

De gemiddelde leeftijd wordt gestaag hoger en de standaardafwijking verandert weinig.

Ja.

(bron: "Onderwijswacht Gelders onderzoek" - Arbon 1994)

Opgave 18

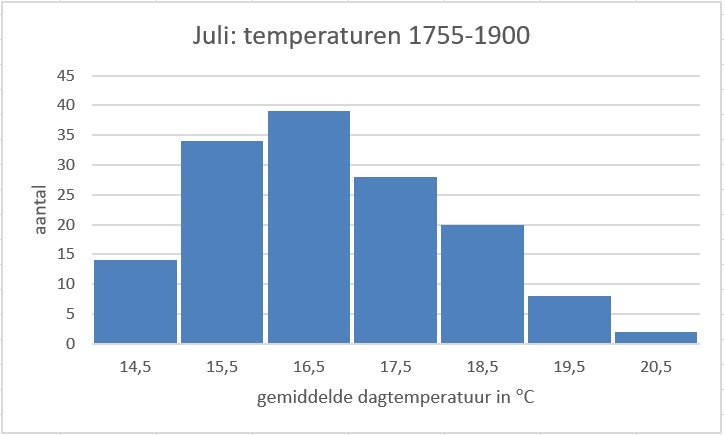
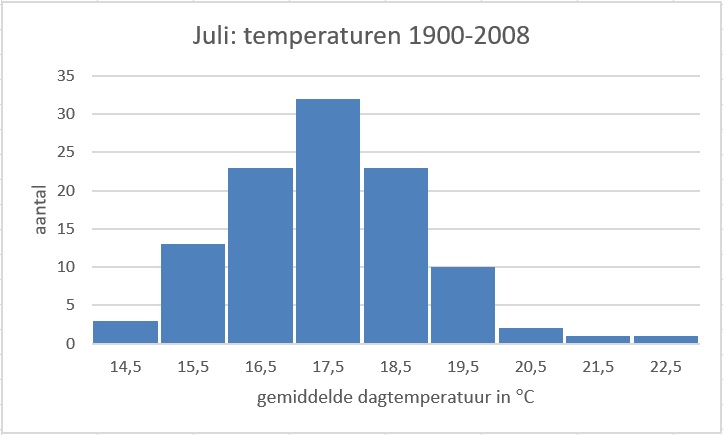
Ja.

| Testen