`0,19`

`0,03 + 0,01 = 0,04`

`T` neemt hier door de manier van meten alleen discrete waarden (gehele minuten) aan.

`T` is de tijd. Ook waarden tussen de hele minuten hebben een betekenis.

Ongeveer zoals een vloeiende kromme door de middens van de bovenkanten van de staven.

Je hebt maximaal `209` seconden (minder dan `3,5` minuten) gewacht, want als je langer had moeten wachten, zou je in de klasse `T = 4` vallen.

`P(T le 3) = 0,16 + 0,19 + 0,19 = 0,54`

De kans is ongeveer `0,44` . Van de laatste staaf telt nu maar ongeveer de helft mee.

`L` kan alle tussenliggende waarden aannemen vanaf ongeveer `100` cm tot ongeveer `250` cm.

`100` %.

De waarde `182` verdeelt de grafiek in twee delen, die vanwege de symmetrie even groot zijn. Het oppervlak onder de hele grafiek is `1` en dus is het oppervlak links van de waarde `182` gelijk aan `0,5` .

Gebruik de vuistregels. Beide waarden liggen precies één standaardafwijking van het gemiddelde, dus: `text(P)( 175 le L le 189 ) ~~ 0,68` .

Gebruik de vuistregels. `189` ligt precies één standaardafwijking boven het gemiddelde, dus boven de `189` ligt nog `(100-68)//2=16` % en: `text(P)(L le 189 ) ~~ 1-0,16 = 0,84` .

Ongeveer `0,1 +0,7 +3,4 +4/5*11,6 ≈ 13,5` %

NB: Omdat 174 niet een waarde is die eenmaal of tweemaal de standaardafwijking afwijkt van het gemiddelde, kun je voor deze schatting niet de vuistregels gebruiken.

De transactietijd is niet symmetrisch verdeeld. Veel transacties kunnen snel worden afgehandeld (vanwege klantvriendelijkheid en/of kosten); weinig transacties duren erg lang.

Uit de grafiek blijkt dat deze kans (weergegeven door de oppervlakte onder de grafiek, rechts van waarde `10` ) vrijwel `0` is.

Gebruik de staafjes met breedte `1` om de oppervlakte onder de kromme lijn te schatten.

`text(P)(T ≤ 4,5) ~~ 0,16 + 0,18 + 0,18 + 0,15 + 1/2 * 0,12 = 0,73` .

Dit is normaal verdeeld.

Dit is normaal verdeeld.

Waarschijnlijk is dit niet normaal verdeeld, het gewicht is sterk te beïnvloeden door (slechte) eetgewoontes.

Dit is niet normaal verdeeld, er zijn veel meer lagere inkomens dan topinkomens, de verdeling is erg scheef.

Dit is niet normaal verdeeld, kleinere wachttijden zullen vaker voorkomen dan grotere.

Stel in `mu(L) = 182` en `sigma (L) = 7` .

Lees uit de applet af: `Ρ(L lt 182 - 14) ~~ 0,022` en `Ρ(L lt 182 + 14) ~~ 0,976` .

Het verschil is ongeveer `0,976 - 0,022 = 0,954` en dat is `95` %.

Dit percentage is ongeveer gelijk aan `(0,5 * 95) - (0,5 * 68) ~~ 13,5` %

Zie figuur.

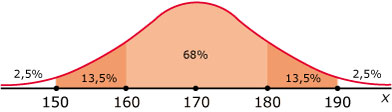
Bijna `100` %.

I: `2,5` %, II: `13,5` %, III: `34` %, IV: `34` %, V: `13,5` %, VI: `2,5` %.

Dat is het oppervlak van categorie V en VI samen.

Dus `16` %.

Dat is het oppervlak van categorie III, IV en V  samen.

Dus `81,5` %.

Dat is het oppervlak van categorie III, IV, V en VI samen.

Dus `84` %.

Zie de figuur (gebruik vuistregels, symmetrie en totaal is `100` %).

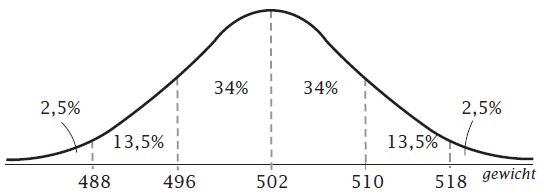
Grofweg `68` % van de pakken wijkt minder dan één standaardafwijking af van het gemiddelde. Dat betekent dat er nog ongeveer `32` % van de pakken meer dan één standaardafwijking afwijken van het gemiddelde.

`510` is het gemiddelde plus eenmaal de standaardafwijking: ongeveer `50 + 1/2 * 68 = 84` % van de pakken heeft een gewicht van minder dan `510`  gram.
Zie eventueel de tekening bij a.

Nee nu nog niet, de vuistregels zijn hierbij niet te gebruiken.

`500` ligt in het gebied tussen `μ - σ = 494` en `μ = 502` , dat ongeveer `34` % van de pakken betreft.

Het stuk onder de kromme tussen `494` en `500` is ruim de helft van de totale `34` %, dus grofweg `20` %. In totaal weegt dus grofweg `2,5 + 13,5 + 20 = 36` % van de pakken minder dan `500`  gram. Dat is meer dan een derde van de pakken, dus hebben de klagers gelijk.

`17` van de `30` pakken zijn afgerond lichter dan `1000`  gram.
Dat is ongeveer `56,7` % van de pakken.

Gebruik je GR of gebruik Excel.

Als je een vloeiende lijn door het midden van de bovenkant van alle staafjes zou tekenen, wordt het histogram bij benadering wel een klokvorm.

Voer de lijst met de dertig gewichten op de grafische rekenmachine in en laat de statistische berekeningen uitvoeren. Dit geeft: `bar x ~~ 998,9` en `σ ~~ 2,5` gram.

Je kunt dit ook op basis van de klassenindeling laten berekenen: afgerond op één decimaal komen er dezelfde waarden uit.

Gebruik de vuistregels van de normale verdeling.

De figuur met `x` -waarden: `mu = 3,0` en `mu+sigma = 3,2` , dus `σ = 0,2` .
De figuur met `k` -waarden: `mu+sigma = 88` en `mu-sigma = 76` , dus `μ = 82` en `σ = 6` .

Gebruik de vuistregels van de normale verdeling.

De figuur met `x` -waarden: een gebied van `16` %.
De figuur met `k` -waarden: een gebied van `84` %.

Bedenk: `85 = μ - σ` en `115 = μ + σ` .
De eerste vuistregel zegt dat grofweg `68` % van de waarden ligt tussen `85` en `115` .

Bedenk: `130 = μ + 2σ` .

Vuistregel: grofweg `95` % van de waarden ligt tussen `μ - 2σ` en `μ + 2σ` .

Het gaat hier dus om het oppervlak rechts van het `95` %-gebied.

In dat gebied zit `(100-95)//2 = 2,5` % van de mensen.

`100 - 2,5 = 97,5` %

Dit `16` %-gebied zit links van `mu-sigma` .

Dan heb je een IQ dat lager is dan `85` .

Gemiddeld heeft een 16-jarige een score van `56` . De vraag is: hoe groot is de kans dat een 12-jarige hoger scoort dan `56` ?

Voor een 12-jarige is de score `56` gelijk aan `μ + σ` , de rechtergrens van het `68` %-gebied.

Vanwege de vuistregels van de normale verdeling is de gevraagde kans daarom ongeveer gelijk aan `1/2 * (100 - 68) = 16` %.

Bedenk:

• Normaalkrommen liggen volgens de vuistregels grofweg tussen `μ - 3σ` en `μ + 3σ` .

• De normaalkromme van de 12-jarigen heeft een hogere top omdat de standaardafwijking het kleinst is (en de afstand tussen `μ - 3σ` en `μ + 3σ` daardoor ook het kortst is) en beide normaalkrommen toch een even grote oppervlakte onder zich moeten hebben (beide `100` %).

Maak eerst een frequentietabel (bij voorkeur in Excel) met klassenindeling, startend met `996,0 - <997,0` en laat vervolgens het histogram aanmaken (of teken het zelf op papier).

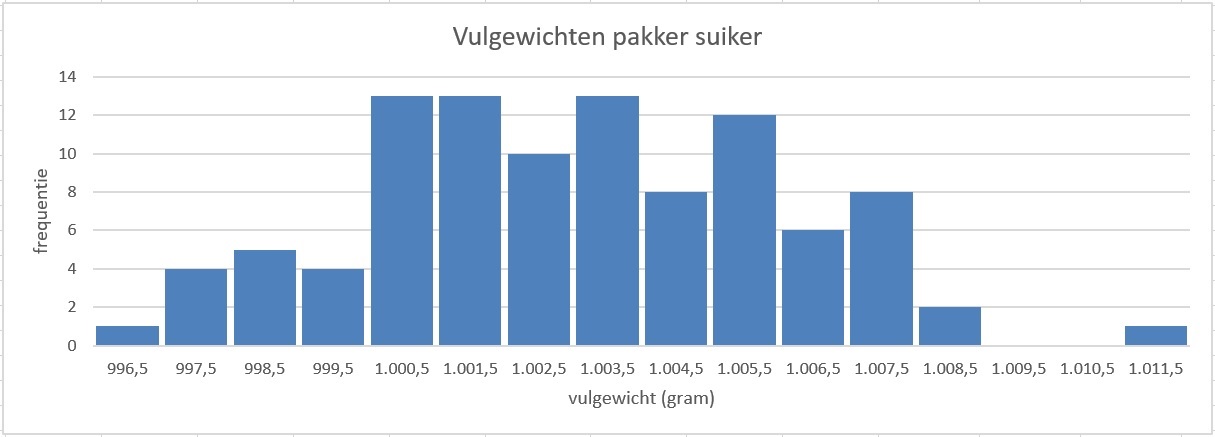
Er ontstaat geen mooie symmetrische klokvorm.

Gebruik Excel: `bar x ≈ 1003` en `σ ≈ 3` gram.

Volgens het histogram zijn dat er `2 + 6 + 2 = 8` van de honderd pakken: `8` %.

1000 gram is het gemiddelde min één keer de standaardafwijking. Volgens de eigenschappen/vuistregels van de normale verdeling heeft `1/2 * (100 - 68) = 16` % van de pakken een lager gewicht dan `1000`  gram.

De eerste vuistregel zegt dat grofweg `68` % van de waarden minder dan één standaardafwijking van het gemiddelde afligt of, formeler: dat ongeveer `68` % van de waarden tussen `μ - σ` en `μ + σ` ligt.

Deze pakken hebben dus gewichten vanaf `1001` tot en met `1005` gram. Dat zijn er `56` van de `100` . Dus slechts `56` %.

`μ = 162` cm en `σ = 6,5` cm.

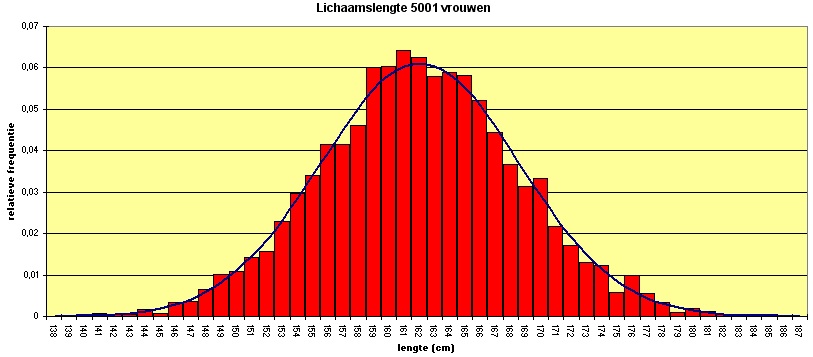
`L` , de lichaamslengte van vrouwen, is een continue statistische variabele, want `L` kan in principe alle gehele en niet gehele lengtewaarden in cm aannemen.

Volgens de tweede vuistregel ligt `95` % van de waarden tussen `μ-2σ` en `μ+2σ` .

Dus `a` is gelijk aan `2σ = 2*6,5 = 13` .

Gebruik de vuistregels weer: `168,5` cm.

`50` %

Ongeveer `84` %.

`μ_B = 1150` en `σ_B = 50` (uur).

Omdat de verdeling breder is ( `σ_B = 50` en dus meer dan twee keer zo groot dan `σ_A` ) en het gebied in beide gevallen `100` % voorstelt, moet de hoogte minder zijn.

`2,5` %

Zie figuur.

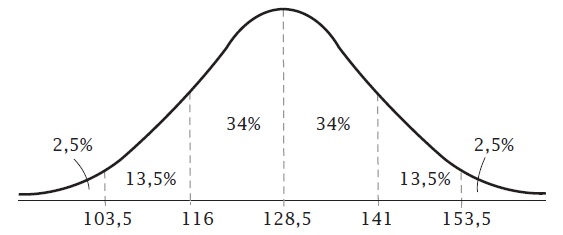
`84` %

`5` %

Nee, de vuistregels zijn hierbij niet te gebruiken.