Antwoorden van de opgaven
Nee, toppen kunnen ook lokale "hoogtepunten" of "dieptepunten " zijn.
Ja, je mag bijvoorbeeld in de formule `y=sqrt(x)` geen negatieve getallen voor `x` nemen.
En de functie kan ergens over gaan, bijvoorbeeld lengtes, breedtes, etc., mogen niet negatief zijn.
Eigen antwoord, houd rekening met het feit dat er functies bestaan waarbij je sommige `x` -waarden niet mag gebruiken. Zoals bijvoorbeeld bij `f(x)=1/x` en `g(x)=sqrt(x)` .

Van boven naar beneden:
`⟨text(-)2 , →⟩`
`⟨←, 2 ]`
`[text(-)2 , 4 ⟩`
`⟨←; 5,5 ]`
`langle larr, 0 rangle uu langle 3,5; rarr rangle`
`x` kan alle reële waarden aannemen, dus `text(D)_(f)=ℝ` .
Los voor de snijpunten met de `x` -as de vergelijking `f(x)= 4-x^2 =0` op. Je vindt: `x=+-2` .
Snijpunten `x` -as: `(text(-)2 , 0)` , `(2 , 0 )` .
`f(0)=4` dus snijpunt `y` -as is: `(0 , 4 )` .
De grafiek is een bergparabool met de top `(0, 4)` , dus `text(B)_(f)=〈←, 4 ]` .
Bekijk de grafiek van `f` op dit interval. Het hoogste punt is `(0, 4)` en het laagste punt is `(3, text(-)5)` . Dus `text(B)_(f)=[text(-)5 , 4 ]` .

`text(D)_(T)=langle 0 , 2000 rangle`
`text(B)_(T)={0,60 ; 1,20 ; 1,80 ; 2,40 ; 3,00 ; 3,60 }`
`x≥0` en `text(D)_(f)=[0 ,→rangle` .
`f(0) = 1`
, dus het snijpunt met de
`y`
-as is
`(0, 1)`
.
`f(x) = 0`
geeft
`sqrt(x) = 1`
en dus
`x = 1^2 = 1`
. Het snijpunt met de
`x`
-as is
`(1, 0)`
.
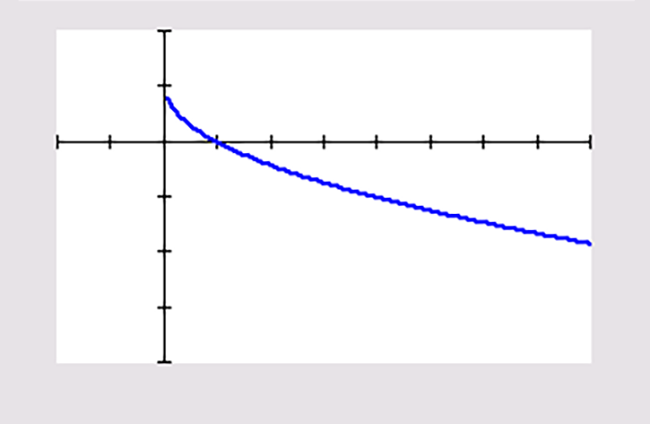
`text(B)_(f)=〈←, 1 ]`
-
`text(D)_(f)=ℝ` en `text(B)_(f)=[text(-)4 ,→〉`
-
`text(D)_(g)=ℝ` en `text(B)_(g)=ℝ`
-
`text(D)_(h)=ℝ` en `text(B)_(h)=[text(-)6,25 ;→〉`
-
`text(D)_(k)=[text(-)7 ,→〉` en `text(B)_(k)=[text(-)6 ,→〉`
Kies het venster `[0, 40] xx [text(-)500, 500]` .
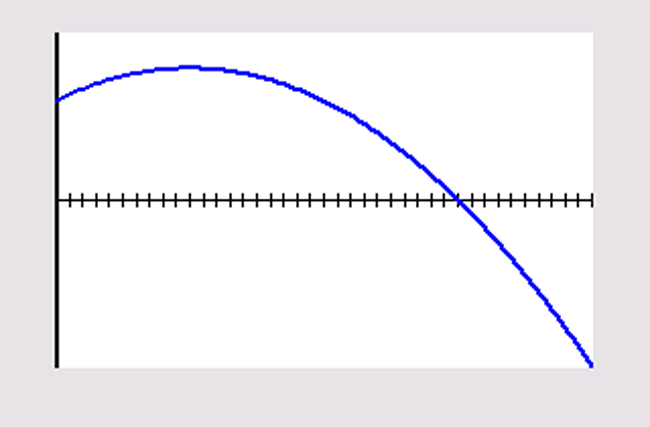
`(10 , 400 )` en aan de randen `(0, 300)` en `(40, text(-)500)` .
`f(0)=300` en `f(40)=text(-)500` .
Het bereik is `[text(-)500, 400 ]` .
Voer in Y1=-3.5X^2+14.7X+0.8 met venster `0 le x le 5` en `0 le y le 20` .
Gebruik voor de nulpunten van het CALC-menu 2: zero. (Of een identieke functies als je een andere grafische rekenmachine hebt dan de TI-84, zie het Practicum.)
Gebruik voor het maximum van het CALC-menu 4: maximum. (Of een identieke functies als je een andere grafische rekenmachine hebt dan de TI-84, zie Practicum.)
Je vindt een maximum van `h=16,235` bij `t ~~ 2,1` .
Los met je grafische rekenmachine op: `h(t)=text(-)3,5t^2+14,7t+0,8 = 10` .
Je vindt `t~~0,765 vv t~~3,435` . De bal is dus ongeveer `3,435-0,765 ~~ 2,67` seconden meer dan `10` m boven de grond.
Er zijn nu geen beperkingen voor
`x`
.
Dus
`text(D)_(f) = RR`
en
`text(B)_(f) = (: larr; 16,235]`
.
`h ( 14 ) = text(-)0,0625(14-6)^2+4 = 0`
`text(D)_(h) = [ 0 , 14 ]`
Bij de top is `h(x)` maximaal. `h(x)` is maximaal als `text(-)0,0625 ( x - 6 ) ^2` zo klein mogelijk is. Dat is het geval als `x-6= 0` , dus als `x=6` .
Invullen geeft: `h(6) = text(-)0,0625 ( 6 - 6 ) ^2+4 = 4` . De top zit dus bij `(6 , 4)` , dus `4` meter boven de grond.
`text(B)_(h) = [ 0 , 4 ]`
`text(D)_(f)=ℝ`
`text(B)_(f)=[text(-)6,25 ;→〉`
`text(D)_(g)=ℝ`
`text(B)_(g)=[text(-)1,62 ;→〉`
`text(D)_(h)=ℝ`
`text(B)_(h)=ℝ`
`text(D)_(f) = [1,5; rarr:)`
`text(B)_(f) = [1, rarr:)`
Voer in: Y1=-2(X-10)^2+60.
Venster bijvoorbeeld:
`[0,40] xx [2000,200]`
.
Optie maximum geeft
`f(10)=60`
en de kleinste functiewaarde is
`f(40)=text(-)1740`
.
`text(B)_(f)=[text(-)1740,60]`
`x^2-2x^4 = x^2(1-2x^2)=0` geeft `x=0 ∨x=text(-)1/2sqrt(2 ) vv x=1/2sqrt(2)` .
Venster bijvoorbeeld:
`[text(-)1,5 ; 1,5] xx [text(-)2 ; 1]`
.
Toppen
`(text(-)0,5; 0,125)`
,
`(0, 0)`
en
`(0,5; 0,125)`
.
`text(B)_(f)=〈←; 0,125 ]`
`text(B)_(g)=〈←, 0 ]`
`(text(-)1 , 1 )` , `(0 , 0 )` en `(1 , 1 )`
`80` meter na `4` seconden.
`text(D)_(h)=[0 , 6 ]`
`text(B)_(h)=[0 , 80 ]`
`60` meter
Voer in: Y1=40X-5X^2 en Y2=40.
Venster bijvoorbeeld:
`[0, 6]xx[0, 100]`
.
Er is één snijpunt (let op het domein). De optie intersect geeft
`x~~1,17`
.
De vuurpijl is ongeveer
`6-1,17=4,83`
seconden boven
`40`
meter.
`h` is tegen de tijd `t` uitgezet.
`R=p(400 -0,5 p)`
`q ge 0` betekent `400-0,5p ge 0` , hieruit volgt `0,5p le 400` en dus `p le 400/(0,5)=800` .
`p` kan alle waarden aannemen in het interval `[0, 800]` .
Voer in: Y1=X(400-0,5X).
Venster bijvoorbeeld:
`[0,800]\times[0,100000]`
.
Je vindt max. `R=80000` .
`R` kan alle waarden aannemen in het interval `text(B)_(R) =[0,80000]` .
`text(D)_(h)=[text(-)5 ,5 ]`
Het minimum is `0` en het maximum is `5` , dat geeft `text(B)_(h)=[0 ,5 ]` .
Waarden tussen `text(-)20` en `20` .
De kortste tuidraad is `5` meter. De langste is `63,32` meter.
`32` meter.
`I(x) = x( 20 - 2 x ) ( 12 - 2 x )`
`text(D)_(I) = (: 0 , 6 :)`
`text(B)_(I) = (: 0 ; 262,68 ]`
`2,43` cm bij `2,43` cm
`text(D)_(f)=ℝ` en `text(B)_(f)=〈←, 4 ]`
`text(D)_(g)=ℝ` en `text(B)_(g)={4 }`
`text(D)_(h)=〈← , 4]` en `text(B)_(h)=[2 ,→〉`
`y(3 )=y(text(-)3 )=9`
`x=0 ∨ x=sqrt(8) ∨ x=text(-)sqrt(8)`
`(text(-)2 , text(-)16 )` , `(0, 0 )` en `(2 , text(-)16 )` . Het bereik is `[text(-)16, →⟩`