Functies en grafieken > Domein en bereikVerwerken
Bepaal van de volgende functies het domein en het bereik. Noteer ze als interval met eventuele benaderingen in twee decimalen nauwkeurig.
`f(x)=x^2-x-6`
`g(x)=x^2(x-2 )(x-3 )`
`h(x)=x^3-6 x`
`k(x)=1 +2 sqrt(2x - 3)`
Gegeven is de functie `f` met `f(x)=text(-)2 (x-10 ) ^2+60` met domein `[0 , 40 ]` .
Bepaal het bereik van `f` .
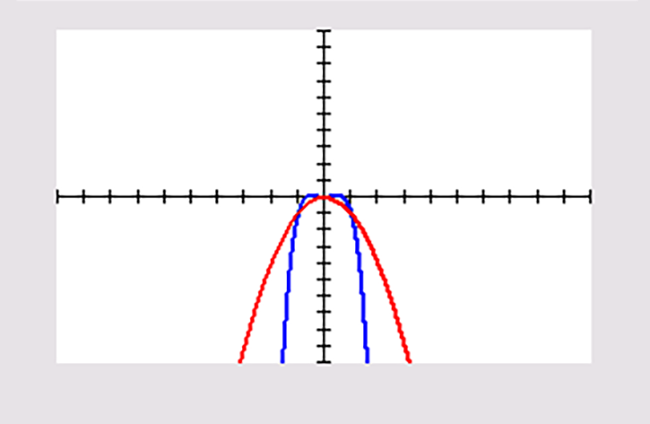
Je ziet de grafieken van de functies `f` en `g` met `f(x)=x^2-2 x^4` en `g(x)=text(-) x^2` met de standaardinstellingen van het venster.
Bereken algebraïsch de nulpunten van `f` .
De standaardinstellingen zijn niet erg gelukkig gekozen als je de toppen en de nulpunten van beide functies wilt zien. Kies betere instellingen en bepaal de toppen van de grafiek van `f` .
Bepaal van beide functies het bereik.
Bereken algebraïsch de snijpunten van de grafieken van `f` en `g` .
Een vuurpijl wordt vanaf de grond afgeschoten. De hoogte boven de grond hangt af van de tijd tot hij uit elkaar spat. Er geldt: `h(t)=40 t-5 t^2` . Hierin is `h` de hoogte boven de grond in meter en `t` de tijd in seconden.
De vuurpijl spat na `6` seconden uit elkaar. Hoe hoog komt hij maximaal?
Schrijf het domein en bereik van deze functie op, rekening houdend met de beschreven situatie.
Op welke hoogte spat de vuurpijl uit elkaar?
Hoeveel seconden is de vuurpijl hoger dan `40` meter hoogte?
Waarom is de getekende grafiek niet de baan van de vuurpijl?
Een handelaar heeft wekelijks
`400`
exemplaren van een bepaald product in de verkoop. Hij heeft geen concurrentie, dus de hoeveelheid
`q`
die hij verkoopt, hangt alleen af van de prijs
`p`
die hij per exemplaar vraagt.
Er geldt:
`q=400 -0,5 p`
.
Geef een formule voor de opbrengst `R` als functie van de prijs `p` .
Welke waarden kan `p` aannemen?
Welke waarden kan `R` aannemen?
De boog onder een brug heeft de vorm van de grafiek van `h(x)=sqrt(25 -x^2)` (met `x` en `h` in meter).
Welke waarden voor `x` kun je hier invullen?
Wat zijn de maximale en de minimale waarden van `h` ?