Functies en grafieken > Domein en bereikVoorbeeld 2
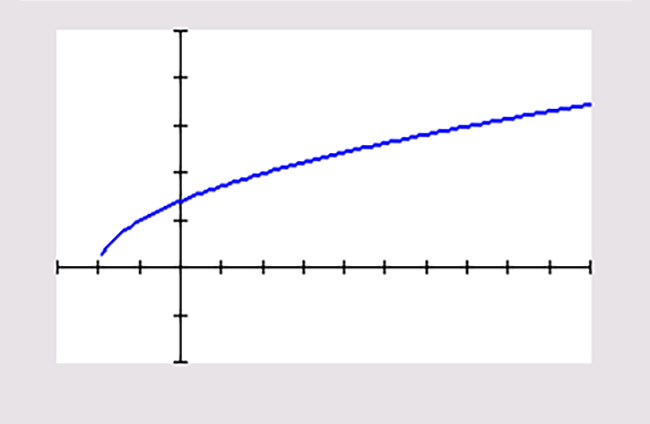
Breng met de grafische rekenmachine de grafiek van `f(x)=sqrt(x+2 )` goed in beeld. Geef het domein en bereik van `f` .
Je kunt niet de wortel nemen van een negatief getal. Dus er moet gelden dat `x + 2 \ge 0` en hieruit volgt dat `x \ge text(-)2` . Het kleinste getal dat mogelijk is als invoerwaarde is `x=text(-)2` . Je krijgt dan als functiewaarde `f(text(-)2 )=sqrt(text(-)2 +2 )=0` . En verder worden de functiewaarden langzaam groter naarmate je een groter getal voor `x` kiest.
De gebruikte vensterinstelling is `[text(-)3 , 10 ]xx[text(-)2 , 5 ]` .
|
|
|
Het wortelteken in het functievoorschrift bepaalt het domein en het bereik.
-
De wortel uit een negatief getal is niet reëel, dus `text(D)_(f)=[text(-)2 ,→⟩` .
-
De functiewaarden zijn `0` of groter, dus `text(B)_(f)=[0 ,→⟩` .
Gegeven is de functie `f` met `f(x)=1 -sqrt(x)` .
Welke waarden kan `x` aannemen? Schrijf het domein van `f` op.
Bereken algebraïsch de snijpunten van de grafiek van `f` met de assen.
Bekijk de grafiek van `f` . Schrijf het bereik van `f` op.
Je ziet vier grafieken van een functie. Alle toppen en nulpunten zijn in beeld.
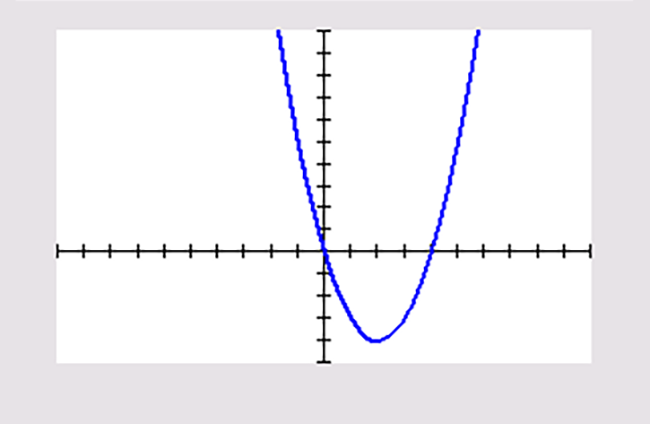
`f(x)=x^2-4 x` |
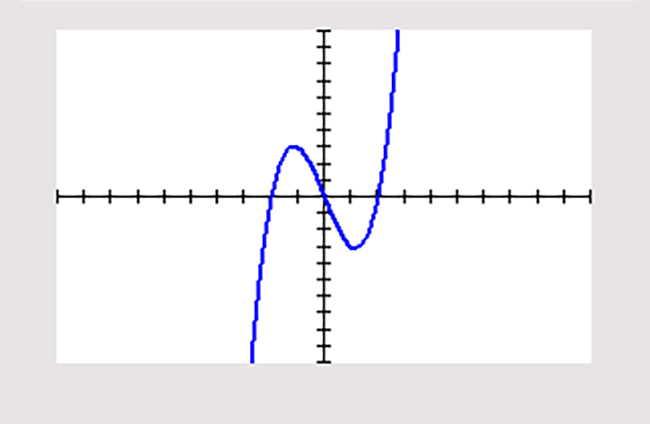
`g(x)=x^3-4 x` |
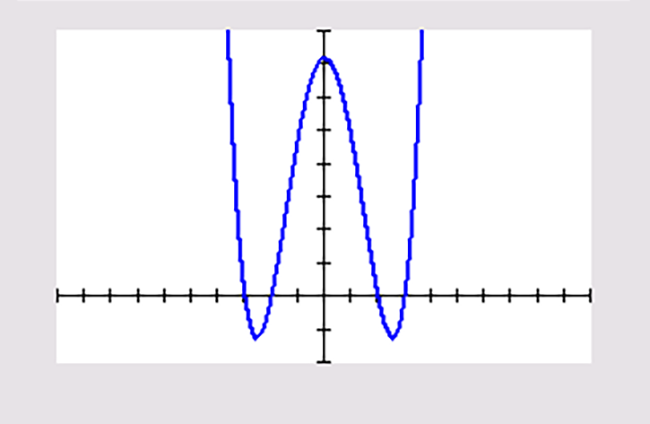
`h(x)=(x^2-4 )(x^2-9 )` |
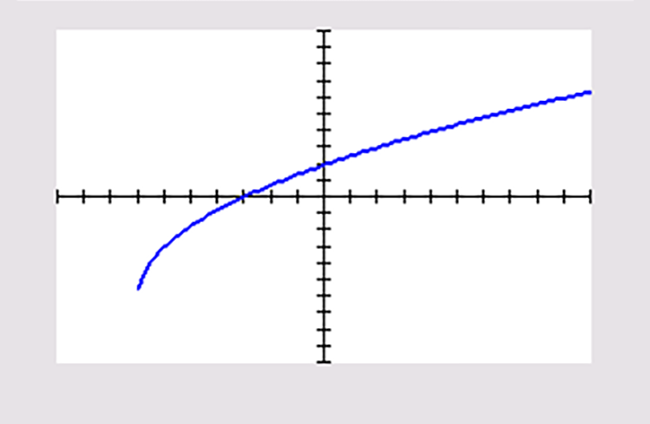
`k(x)=text(-)6 +3 sqrt(x+7 )` |
Schrijf het domein en bereik van deze functies op. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
Gegeven is de functie `f(x)=400 - (x-10 ) ^2` . Het domein van deze functie is `[0 , 40 ]` .
Breng de grafiek met de grafische rekenmachine goed in beeld. Bekijk eventueel Voorbeeld 2 of het practicum nog eens.
Geef de coördinaten van de toppen van `f` .
Bepaal het bereik van `f` . (Let op het gegeven domein!)