Functies en grafieken > Domein en bereikVoorbeeld 3
Een keeper schopt de bal in de lucht. Voor de hoogte van de bal
`h`
in meter na
`t`
seconden geldt
`h(t)=text(-)3,5t^2+14,7t+0,8`
.
Benader het domein en bereik van
`h`
in twee decimalen nauwkeurig.
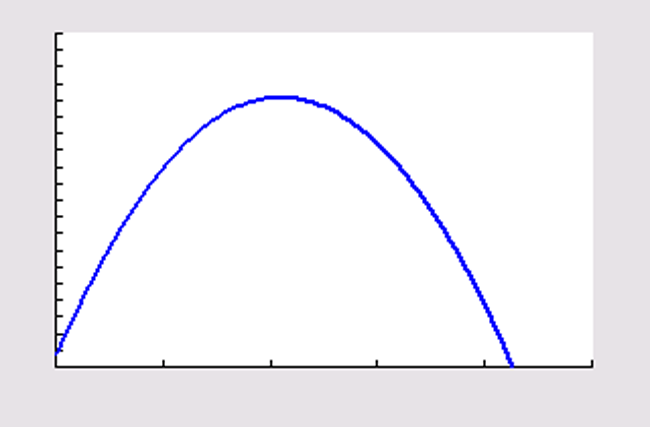
De grafiek van `h` is een bergparabool en het domein en bereik daarvan worden bepaald door de situatie.
Je weet dat `t ge 0` . Verder snijdt de grafiek de horizontale as bij `t~~4,25` . Dus het domein (afgerond op twee decimalen) is `[0; 4,25]` .
Voor het bereik moet je de top van de grafiek bepalen. Met de grafische rekenmachine vind je dat er een maximum is van `16,235` . Omdat de bal op de grond komt is de minimale waarde `0` . Dus het bereik is `[0; 16,235]` .
Bekijk Voorbeeld 3.
Maak zelf de grafiek van de gegeven functie en laat je grafische rekenmachine de twee nulpunten berekenen.
Bepaal ook het maximum van deze functie met behulp van de grafische rekenmachine.
Bereken hoeveel seconden de bal meer dan
`10`
meter boven de grond is.
Geef je antwoord in twee decimalen nauwkeurig.
Schrijf nu ook het domein en het bereik op van de functie `f(x)=text(-)3,5x^2+14,7x+0,8` zonder beperkingen voor `x` .
Bekijk de baan van een kogel die door een kogelstoter zo ver mogelijk wordt gestoten. De kogel komt `14` meter ver. Het hoogste punt van de baan zit `4` meter boven de grond. De baan van de kogel kan worden beschreven met de formule `h ( x ) = text(-)0,0625 ( x - 6 ) ^2 + 4` waarin `h` de hoogte van de kogel boven de grond is en `x` de afstand is die het punt op de grond recht onder de kogel heeft afgelegd vanaf het moment van loslaten.
Laat zien dat de kogel inderdaad `14` meter ver komt.
Welke invoerwaarden zijn hier zinnig? Schrijf het domein van `h(t)` op.
Laat zien dat het hoogste punt van de baan inderdaad `4` meter boven de grond zit.
Welke functiewaarden zijn hier zinnig? Schrijf het bereik van deze functie op.