Periodieke functies > RadialenVoorbeeld 2
Bepaal met de rekenmachine
`sin(1)`
,
`sin(10)`
,
`sin(1/6 π), sin(360)`
en
`sin(10+30pi)`
.
Welke waarden zijn hetzelfde?
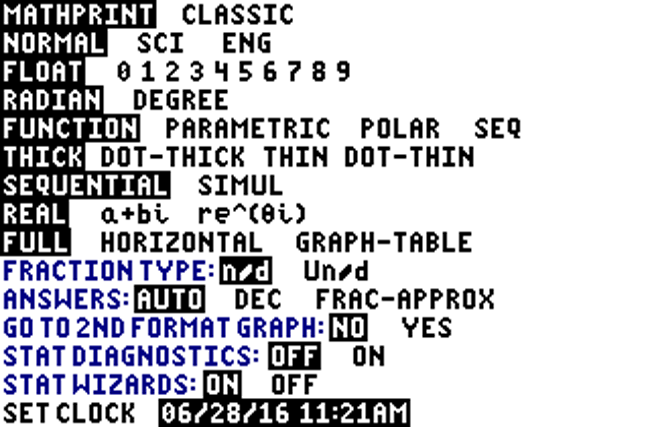
Reken in radialen, want er zijn geen gradentekens. Laat de rekenmachine dan ook in radialen rekenen.
Ga na dat:
`sin(1) ≈ 0,841`
`sin(10) ≈ text(-)0,544`
`sin(1/6 π) = 0,5`
`sin(360) ≈ 0,959`
`sin(10+30pi) ~~ text(-)0,544`
De uitkomsten van `sin(10)` en `sin(10+30pi)` zijn gelijk omdat tussen `10` en `10+30pi` precies `30pi` zit. Dat is precies `15` keer één volledige cirkel (lengte `2pi` ).
Bekijk Voorbeeld 2.
Bepaal in drie decimalen nauwkeurig `sin(1/55 pi)` .
Leg uit waarom `sin(40 1/55 pi)` dezelfde uitkomst geeft.
Geef nog twee verschillende waarden voor `x` waarvoor geldt: `sin(1/55 pi)=sin(x)` .
De draaihoeken kun je ook gewoon `x` noemen. Dat is later handig als je grafieken van de sinusfunctie en de cosinusfunctie gaat maken.
Leg uit waarom `sin(x) = sin(x+k*2 π)` en `cos(x) = cos(x+k*2pi)` , waarbij `k` een geheel getal is.
Welke waarden kunnen `sin(x)` en `cos(x)` aannemen?
Waarom is `sin(1/6 π)` exact `1/2` ?
Geef de volgende waarden exact: `sin(5 1/6 π)` , `cos(text(-)1 5/6 π)` , `sin(2 3/4 π)` .