Veranderingen > DifferentiaalquotiëntVoorbeeld 1
Gegeven is de functie
`f`
met
`f(x) = 4 - x^2`
.
Bereken het differentiaalquotiënt voor
`x = 1`
en beschrijf de betekenis van dit getal.
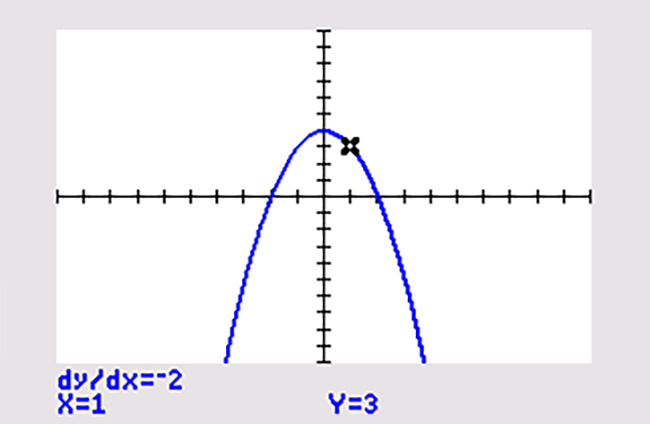
Maak een rij met differentiequotiënten door bij het interval `[1, 1+h]` voor `h` steeds kleinere waarden te kiezen. Bijvoorbeeld:
| interval | differentiequotiënt |
| `[1; 1,1]` | `text(-)2,1` |
| `[1; 1,01]` | `text(-)2,01` |
| `[1; 1,001]` | `text(-)2,001` |
| `[1; 1,0001]` | `text(-)2,0001` |
Deze rij getallen lijkt te naderen naar `text(-)2` . Dit is het differentiaalquotiënt van deze functie voor `x = 1` en de veranderingssnelheid van de grafiek voor die waarde van `x` . Het is ook het hellingsgetal van de raaklijn aan de grafiek voor `x = 1` . Je ziet in de figuur dat een grafische rekenmachine dit voor je kan berekenen, zie ook het Practicum.
In Voorbeeld 1 zie je hoe je bij een gegeven functie `f` het differentiaalquotiënt voor een bepaalde `x` -waarde kunt berekenen.
Wat betekent dit getal voor de grafiek? Meerdere antwoorden kunnen goed zijn.
De richtingscoëfficiënt van de grafiek voor die `xtext(-)` waarde.
De richtingscoëfficiënt van het lijnstuk op het interval `[0, x]` .
De richtingscoëfficiënt van de raaklijn aan de grafiek voor die `x` -waarde.
De `y` -waarde bij die waarde van `x` .
Welke betekenis heeft dit getal voor de functiewaarden?
De grootte van de functiewaarde bij die waarde van `x` .
De snelheid waarmee de functiewaarden veranderen voor die waarde van `x` .
De gemiddelde verandering van de functiewaarden.
Bekijk Voorbeeld 1. Je wilt het differentiaalquotiënt van `f` bepalen voor `x=2` .
Maak zelf de tabel met differentiequotiënten op het interval `[2, 2 +h]` waarin `h` achtereenvolgens de waarden `0,1` ; `0,01` ; `0,001` en `0,0001` heeft.
Hoe groot is dus het differentiaalquotiënt voor `x = 2` ?
Welke vergelijking heeft de raaklijn aan de grafiek van `f` voor `x = 2` ?