Veranderingen > DifferentiaalquotiëntVoorbeeld 3
Gegeven is de functie `f(x) = x^2` . Bereken het differentiaalquotiënt voor `x = 1` zonder een rij met differentiequotiënten te maken.
Het differentiequotiënt op het interval
`[1, 1+h]`
is:
`(Δf(x))/(Δx) = ((1 + h)^2 - 1^2)/h = (1 + 2h + h^2 - 1)/h = (2h + h^2)/h = 2 + h`
Dit differentiequotiënt heeft voor elke waarde van `h` (behalve `h = 0` ) de waarde `2 + h` . Hoe dichter `h` bij `0` komt, hoe dichter `2 + h` bij `2` komt. Dit betekent dat het differentiaalquotiënt voor `x = 1` gelijk is aan `2` .
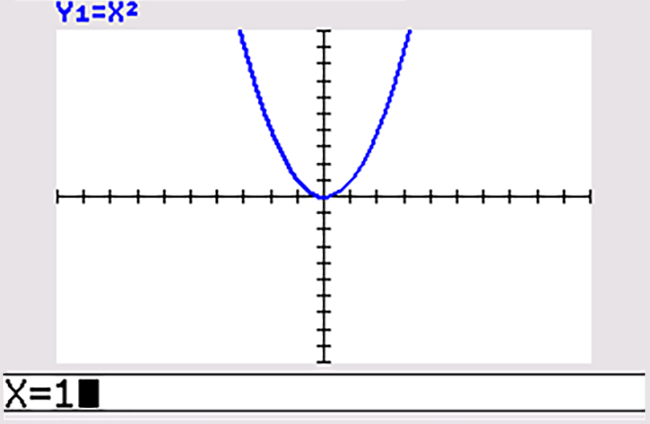
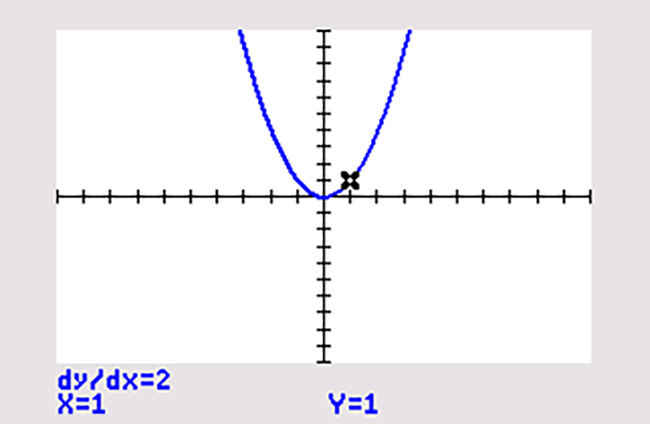
Ook met de grafische rekenmachine kun je het differentiaalquotiënt `(text(d)y)/(text(d)x)` voor `x = 1` meteen vinden:
|
|
|
In Voorbeeld 3 zie je de functie `f(x) = x^2` .
Bereken het differentiequotiënt op het interval `[2, 2+h]` en benader hiermee het differentiaalquotiënt voor `x=2` .
Controleer je antwoord bij a met de grafische rekenmachine.
Stel een vergelijking op voor de raaklijn aan de grafiek voor `x = 2` .
Er is een punt op de grafiek waarin de helling van de raaklijn precies het tegenovergestelde is van die bij a. Welk punt is dat? Licht je antwoord toe.
In welk punt van de grafiek is de helling `0` ?