Testen

Bekijk de grafiek van de functie `f(x) = x^3 - 3x^2 - 9x` , gemaakt met GeoGebra.
Van welke soort daling is er sprake op het interval `[0 , 1]` ?
Bereken het differentiequotiënt op dit interval en beschrijf de betekenis van dit getal.
Bereken de helling van de grafiek in het punt met `x = 1` met een rij differentiequotiënten. Controleer je antwoord met de grafische rekenmachine.
Stel de vergelijking op van de raaklijn aan `f` in het punt met `x=1` .
Neem de grafiek over en schets de hellingsgrafiek bij deze functie.
De hoogte van een vuurpijl die je van de grond afschiet, wordt gegeven door `h(t) = 60t - 5t^2` met `h` de hoogte in meters en `t` de tijd in seconden na het afschieten.
Na `10` seconden ontploft de vuurpijl. Op welke hoogte is dat?
Teken een bijpassend toenamediagram van `0` tot `6` met stapgrootte `1` .
Uit het toenamediagram kun je aflezen op welk tijdstip de vuurpijl het hoogste punt in zijn baan bereikt. Leg uit hoe.
Bereken de gemiddelde snelheid van de vuurpijl over de eerste zes seconden.
Teken de grafiek van de snelheid `h'(t)` van de vuurpijl. Maak eerst een tabel met hellingsgetallen.
De grafiek van de snelheid die je bij e hebt getekend moet een rechte lijn zijn. Stel bij die rechte lijn een formule op en bereken met die formule de snelheid op het moment van ontploffen.
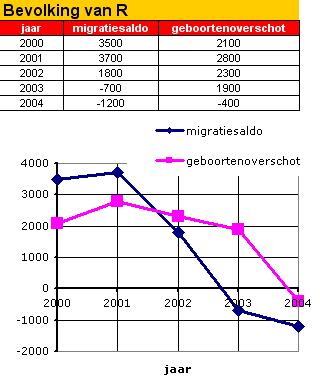
Het migratiesaldo van R geeft het verschil tussen het aantal mensen dat in R komt wonen en het aantal mensen dat uit R vertrekt. Het geboorteoverschot is het verschil van het aantal geboorten en het aantal overledenen in R. In deze grafiek zie je beiden voor de jaren 2000 tot en met 2004.
Met hoeveel mensen is het aantal inwoners in R in het jaar 2000 toegenomen?
In welk jaar is het aantal inwoners in deze stad afgenomen?
Het aantal inwoners van R was aan het begin van het jaar 2000 ongeveer `72600` (op honderdtallen afgerond). Teken een grafiek van het aantal inwoners in R in de jaren 2000 tot en met 2004.
Hoe groot was het aantal inwoners op 1 januari 2005?
Gegeven is de functie `f(x) = 0,25x^2 + x` .
Bereken met het differentiequotiënt op het interval `[2 , 2+h]` exact het differentiaalquotiënt voor `x=2` .
Bepaal de formule van de hellingsfunctie met behulp van een differentiequotiënt.
Gegeven is de functie `f` door `f(x) = 0,5x^3 - 1,5x^2 - 2x` .
Bereken algebraïsch de snijpunten van de grafiek van `f` met de `x` -as. Noem de snijpunten van links naar rechts `A` , `B` en `C` .
Op de grafiek van `f` ligt een punt `D` met `x_D` precies midden tussen `x_A` en `x_B` .
Toon aan dat `CD` de raaklijn is in punt `D` .