Differentieerregels > De quotiëntregelVoorbeeld 3
Bekijk het deel van de grafiek van
`f(x) = (4x)/(x^2+4)`
.
Er zijn twee extremen. Bereken die met behulp van de afgeleide van
`f`
.
De afgeleide is:
`f′(x) = (4*(x^2+4) - 4x*2x)/((x^2+4)^2) = (text(-)4x^2+16)/((x^2+4)^2)`
.
`f'(x) = 0`
geeft
`text(-)4x^2 + 16 = 0`
.
En deze vergelijking levert op:
`x = text(-)2 vv x = 2`
.
Uit de grafiek kun je dan aflezen dat de extremen zijn: max.
`f(2) = 1`
en min.
`f(text(-)2) = text(-)1`
.
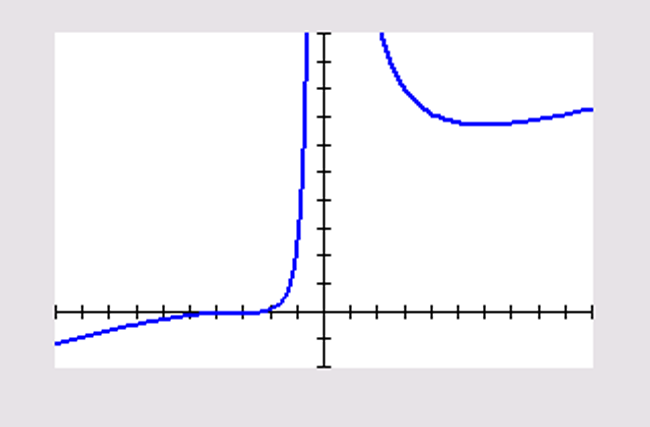
Je ziet hier een deel van de grafiek van `f(x) = ((x+3)^3)/(3x^2)` .
Toon aan dat `f'(x) = ((x - 6)(x + 3)^2)/(3x^3)` .
Bereken het minimum van `f` .
Waarom is het punt `(text(-)3, 0)` een buigpunt van de grafiek van `f` ?