Functie `f` ontstaat uit de standaardfunctie `y = ln(x)` na een vermenigvuldiging ten opzichte van de `x` -as met `text(-)3` , waarbij de grafiek horizontaal gespiegeld is en een horizontale translatie van `text(-)2` .
De asymptoot vind je daarom bij `x = text(-)2` . Door de horizontale spiegeling verandert de limiet bij de asymptoot:

`lim_(x downarrow text(-)2) f(x) = oo`

Functie `g` ontstaat uit de standaardfunctie `y = 1/(x^2)` na een vermenigvuldiging ten opzichte van de `x` -as met `2` , een horizontale translatie van `5` en een verticale translatie van `1` .
De horizontale asymptoot vind je bij `y = 1` en de verticale asymptoot bij `x = 5` .

`lim_(x rarr text(-)oo) g(x) = 1`

`lim_(x rarr oo) g(x) = 1`

`lim_(x uparrow 5) g(x) = oo`
`lim_(x downarrow 5) g(x) = oo`

`h(x) = 3^(2-x) = 3^(text(-)(x-2))`

Functie `h` ontstaat uit de standaardfunctie `y = 3^x` na een vermenigvuldiging ten opzichte van de `y` -as met `text(-)1` , waarbij de grafiek verticaal gespiegeld is en een horizontale translatie van `2` .
De asymptoot is bij `y = 0` gebleven.

`lim_(x rarr oo) h(x) = 0`

`j(x) = 1 - tan(2x) = text(-)tan(2x) + 1`

Functie `j` ontstaat uit de standaardfunctie `y = tan(x)` na een vermenigvuldiging ten opzichte van de `x` -as met `text(-)1` , waarbij de grafiek horizontaal gespiegeld is, een vermenigvuldiging met `1/2` ten opzichte van de `y` -as en een verticale translatie van `1` .

De asymptoten liggen bij `2x = 1/2 pi + k*pi` dus bij `x = 1/4 pi + k*1/2 pi` .

`lim_(x uparrow 1/4 pi + k*1/2 pi)j(x) = text(-)oo` en `lim_(x downarrow 1/4 pi + k*1/2 pi)j(x) = oo` .

De noemer gelijkstellen aan nul geeft: `x^2-1 = 0` .

Dit geeft `x = text(-)1 vv x = 1` .

De twee verticale asymptoten zijn `x = text(-)1` en `x = 1` .

Er geldt `g(x) = x/(x^2-x) = x/(x(x-1)) = 1/(x - 1)` alleen als `x != 0` en `h(0) = text(-)1` , dus de functie `h` heeft wel een waarde voor `x = 0` .

De functie `g` is niet gedefinieerd voor `x = 0` maar `lim_(x↑0) g(x) = text(-)1` en `lim_(x↓0) g(x) = text(-)1` .

Het punt `(0, text(-)1)` is daarmee een perforatie van de grafiek van `f` .

`lim_(x↑1) g(x) = text(-)oo` en `lim_(x↓1) g(x) = oo` .

De lijn `x = 1` is een verticale asymptoot.

`lim_(x rarr text(-)oo) g(x) = 0` en `lim_(x rarr oo) g(x) = 0`

De lijn `y = 0` is een horizontale asymptoot.

Ja, `f` heeft een horizontale asymptoot `y = 0` .
Immers `lim_(x rarr oo) f(x) = lim_(x rarr text(-)oo) f(x) = sin(0) = 0` .

Nee, dat is geen verticale asymptoot.
De grafiek van `f` gaat heel snel heen en weer hoe dichter `x` bij `0` komt, maar blijft altijd tussen `y = text(-)1` en `y = 1` . Het geval wil alleen dat `f` voor `x = 0` ongedefinieerd is.

`f(x) = (x^2+2x-4)/(2x) = (x^2)/(2x) + (2x)/(2x) - (4)/(2x) = 1/2 x + 1 - 2/x`

De functie `f(x) = 1/2 x + 1 - 2/x` en `y = 1/2 x + 1` aan elkaar gelijkstellen geeft:

`1/2x+1-2/x`	`=`	`1/2x+1`
`text(-)2/x`	`=`	`0`

Deze vergelijking heeft geen oplossing. Dat wil zeggen dat `f` de lijn nergens snijdt.

`lim_(x rarr oo) f(x) - (text(-)1/3 x + 25) = lim_(x rarr text(-)oo) f(x) - (text(-)1/3 x + 25) = 0`
De asymptoot is de lijn: `y = text(-)1/3 x + 25` .

`lim_(x rarr text(-)oo)(3x + 1/x - 3x) = lim_(x rarr oo)(3x + 1/x - 3x) = 0`
De asymptoot is de lijn: `y = 3x` .

`h(x) = (x^2+5x+4)/(x+5) = (x^2+5x)/(x+5) + 4/(x+5) = x + 4/(x+5)`
`lim_(x rarr text(-)oo)(x + 4/(x+5) - x) = lim_(x rarr oo)(x + 4/(x+5) - x) = 0`
De asymptoot is de lijn: `y = x` .

Er is geen `x` waarvoor geldt: `text(e)^(3x) = 0` .
Dus de functie kan omgeschreven worden naar:
`f(x) = 1 + 5/(text(e)^(3x)) = 5text(e)^(text(-)3x) + 1`

Functie `f` ontstaat uit de standaardgrafiek `y = text(e)^x` na een vermenigvuldiging ten opzichte van de `x` -as met `5` , een vermenigvuldiging ten opzichte van de `y` -as met `text(-)1/3` , waarbij de grafiek verticaal gespiegeld is en een verticale translatie van `1` .
Er geldt:
`lim_(x rarr oo) f(x) = 1`
De functie heeft de horizontale asymptoot `y = 1` .

`g(x) = ln(text(-)4(x-1/4))`

Functie `g` ontstaat uit de standaardgrafiek `y=ln(x)` na een vermenigvuldiging ten opzichte van de `y` -as met `text(-)1/4` , waarbij de grafiek gespiegeld is en een horizontale translatie met `1/4` .

Er geldt:
`lim_(x uparrow 1/4) h(x)=text(-)oo`
De functie `h` heeft een verticale asymptoot `x = 1/4` .

`h(x) = tan(text(-)1/2(x - 1 1/3 pi))`

Functie `h` ontstaat uit de standaardgrafiek `y = tan(x)` na een vermenigvuldiging met `text(-)2` ten opzichte van de `y` -as, waarbij de grafiek verticaal gespiegeld is en een horizontale translatie van `1 1/3pi` .

Er geldt:
`lim_(x uparrow 1/3 pi + k*2pi) h(x) = text(-)oo` en `lim_(x downarrow 1/3 pi + k*2pi) h(x) = oo` .

De grafiek van `h` heeft verticale asymptoten als `2/3 pi - 1/2 x = 1/2 pi + k*pi` ofwel wanneer `x = 1/3 pi + k*2pi` .

Voor `x! = 0` is de functie te schrijven als: `k(x) = 2/(x+3)` .
Dit is gelijk aan de functie `f` bij a en heeft dus ook dezelfde horizontale en verticale asymptoten.
Er geldt:
`lim_(x uparrow 0) k(x) = lim_(x downarrow 0) k(x) = 2/3`
De functie heeft dus een perforatie op `(0, 2/3)` .

`f(x) = (x+1)/(1-x) = (text(-)x-1)/(x-1) = (text(-)2-(x-1))/(x-1) = (text(-)2)/(x-1)-(x-1)/(x-1) = text(-)2/(x-1)-1`

`lim_(x rarr text(-)oo)f(x) = lim_(x rarr oo)f(x) = lim_(x rarr oo)(text(-)2/(x-1)-1) = text(-)1`

`lim_(x uparrow 1)(x+1)/(1-x) = oo` en `lim_(x downarrow 1)(x+1)/(1-x) = text(-)oo`

De asymptoten zijn de lijnen `y = text(-)1` en `x = 1` .

De functie heeft een asymptoot als `1 - sin(x) = 0`
Hieruit volgt: `sin(x) = 1` ofwel `x = 1/2 pi + k*2pi` .
`lim_(x uparrow 1/2 pi + k*2pi) g(x) = lim_(x downarrow 1/2 pi + k*2pi) g(x) = oo`
De functie `g` heeft verticale asymptoten op `x = 1/2 pi + k*2pi`

De functie `g` heeft geen horizontale asymptoten omdat er geen limiet als `x rarr text(-)oo` of `x rarr oo` bestaat.

Functie `f` is een gebroken functie met in de teller en de noemer veeltermen van `x` . Dit soort gebroken functies heeft een eindig aantal verticale asymptoten en één horizontale asymptoot.

Door het periodieke karakter van de noemer heeft de functie `g` oneindig veel verticale asymptoten.

Daarentegen heeft functie `g` geen horizontale asymptoot omdat `sin(x)` tussen `text(-)1` en `1` blijft schommelen en geen waarde benadert als `x rarr +-oo` .

Venster: `[text(-)10, 10]xx[0, 10]` .

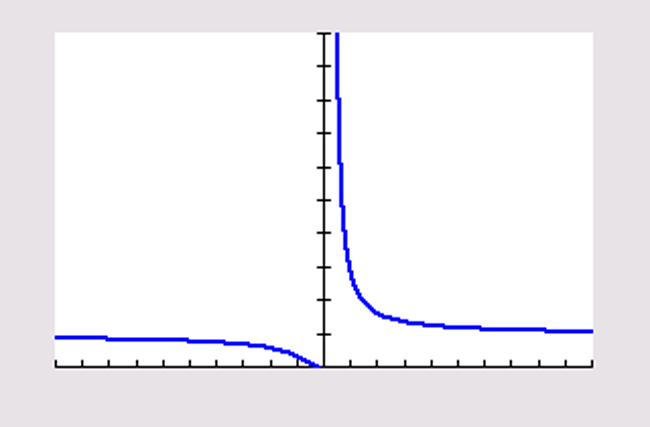
`lim_(x rarr text(-)oo)f(x) = text(e)^0 = 1` en `lim_(x rarr text(-)oo)f(x) = text(e)^0 = 1`

Er is dus een horizontale asymptoot `y = 1` .

Een gebroken functie heeft ook een verticale asymptoot voor de waarde die de noemer nul maakt:
`lim_(x downarrow 0) f(x) = oo` en `lim_(x uparrow 0) f(x) = 0` .
Er is een verticale asymptoot `x = 0` die alleen benaderd wordt voor `x downarrow 0` .

`lim_(x rarr text(-)oo)f(x) - (4x-20) = lim_(x rarr oo)f(x) - (4x-20) = 0`
De vergelijking van de scheve asymptoot is `y = 4x-20`

`lim_(x rarr text(-)oo)g(x) + 2x = lim_(x rarr oo)g(x) = lim_(x rarr oo)(text(-)2x + 4/x + 2x) = 0`

De vergelijking van de scheve asymptoot is `y = text(-)2x` .

`h(x) = (3x^2 - 4x - 2)/(x - 2) = (3x^2 - 6x + 2x - 2)/(x - 2) = 3x + (2x - 2)/(x - 2) = 3x + (2x - 4)/(x - 2) + 2/(x - 2) = 3x + 2 + 2/(x-2)`
`lim_(x rarr text(-)oo)h(x) - (3x+2) = lim_(x rarr oo)(3x + 2 + 2/(x-2) - 3x - 2) = 0`
De vergelijking van de scheve asymptoot is `y = 3x+2`

`lim_(x rarr oo) g(x) - (5-2x) = 0`

De vergelijking van de scheve asymptoot is `y = 5-2x` .

De `text(-)4` is voor grote waarden van `x` te verwaarlozen.

`lim_(x rarr oo)sqrt(x^2-4) - x = lim_(x rarr oo)sqrt(x^2) - x = 0` , omdat `x` positief is.

De vergelijking van de scheve asymptoot is `y = x` .

`lim_(x rarr text(-)oo)sqrt(x^2-4) + x = lim_(x rarr text(-)oo)sqrt(x^2) + x = 0` , omdat `x` negatief is.

De vergelijking van de scheve asymptoot is `y = text(-)x` .

`f(x) = 5/(x-4)` voor `x != 0` .
`lim_(x rarr oo) 5/(x-4) = lim_(x rarr text(-)oo) 5/(x-4) = 0`
`lim_(x uparrow 4) 5/(x-4) = text(-)oo` en `lim_(x downarrow 4) 5/(x-4) = oo`
De functie heeft dus een horizontale asymptoot `y = 0` en een verticale asymptoot `x = 4` .
Verder geldt: `lim_(x uparrow 0) 5/(x-4) = lim_(x downarrow 0) 5/(x-4) = text(-)5/4 = text(-)1 1/4` , maar `f` is niet gedefinieerd voor `x = 0` .
De functie heeft dus een perforatie op `(0, text(-)1 1/4)` .

`g(x) = 3(x+2) = 3x+6` voor `x! = 0` .

`lim_(x uarr 0) g(x) = lim_(x darr 0) g(x) = 6` , maar `g` is niet gedefinieerd voor `x = 0` .
Deze functie heeft een perforatie op `(0, 6)` :

`lim_(x rarr oo) h(x) = lim_(x rarr text(-)oo) h(x) = 0`
`lim_(x uparrow 1) h(x) = lim_(x downarrow 2) h(x) = oo`
`lim_(x downarrow 1) h(x) = lim_(x uparrow 2) h(x) = text(-)oo`
De functie `h` heeft dus een horizontale asymptoot `y = 0` en twee verticale asymptoten `x = 1` en `x = 2` .

`f` heeft verticale asymptoten als `2cos^2(x) - 1 = 0` , ofwel wanneer:
`cos(x) = text(-)1/2 sqrt(2) vv cos(x) = 1/2 sqrt(2)` , dus `x = text(-)1/4 pi + k*pi vv x = 1/4 pi + k*pi` .
`lim_(x uparrow 1/4 pi + k*pi) f(x) = lim_(x downarrow text(-)1/4 pi + k*pi) f(x) = oo`
`lim_(x uparrow text(-)1/4 pi + k*pi) f(x) = lim_(x downarrow 1/4 pi + k*pi) f(x) = text(-)oo`
`f` heeft verticale asymptoten `x = 1/4 pi + k*1/2 pi` .
`f` heeft geen horizontale asymptoot.

De functie heeft verticale asymptoten wanneer `x^2 - 1 = 0` , dus `x = text(-)1 vv x = 1` .
`lim_(x uparrow text(-)1) g(x) = lim_(x downarrow 1) g(x) = text(-)oo` , dus verticale asymptoten `x = text(-)1` en `x = 1` .
`g` heeft geen horizontale asymptoot.

`h` heeft geen asymptoten.

`ln(x) = 0` wanneer `x = 1` dus `k` heeft daar een verticale asymptoot:
`lim_(x uparrow 1) k(x) = text(-)oo` en `lim_(x downarrow 1) k(x) = oo` .
En omdat `lim_(x rarr oo) ln(x) = oo` is `lim_(x rarr oo) k(x) = 0` .
`k` heeft een horizontale asymptoot `y = 0` .

`lim_(x rarr text(-)oo) f(x) - (4x-20) = lim_(x rarr oo) f(x) - (4x-20) = 0` .
De vergelijking van de scheve asymptoot is `y = 4x-20` .

`lim_(x rarr text(-)oo) (g(x) + 2x) = lim_(x rarr oo) (g(x) + 2x) = lim_(x rarr oo) (text(-)2x + 4/x + 2x) = 0` .

De vergelijking van de scheve asymptoot is `y = text(-)2x` .

De exponentiële functie `y = text(e)^x` heeft een horizontale asymptoot als `lim_(x rarr text(-)oo)text(e)^x = 0` .

De grafiek van `y = text(e)^(1-x) = text(e)^(text(-)(x-1))` ontstaat uit de standaardgrafiek `y = text(e)^x` na een vermenigvuldiging ten opzichte van de `y` -as met `text(-)1` en een horizontale translatie van `1` .

Er geldt daarom: `lim_(x rarr oo)text(e)^(1-x) = 0` , zodat: `lim_(x rarr oo)(5-2x+text(e)^(1-x)) = 5-2x` .

De vergelijking van de scheve asymptoot is `y = 5-2x` .

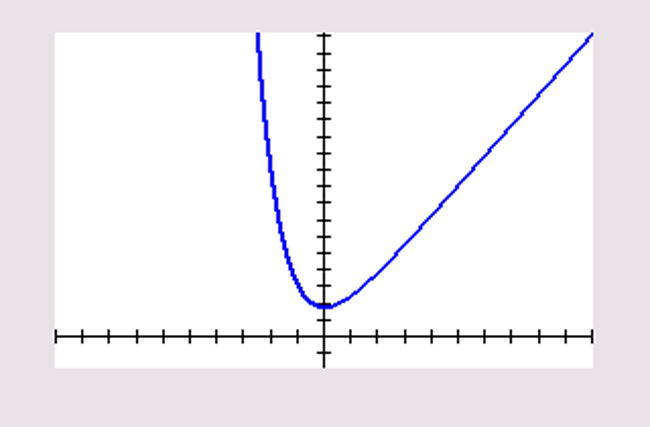
`f(x) = 1/(text(e)^x) + x = text(e)^(text(-)x) + x` .
`lim_(x rarr oo) text(e)^(text(-)x) = 0` , dus `lim_(x rarr oo) f(x) - x = 0` .
De vergelijking van de scheve asymptoot is `y = x` .

De functie lijkt op een parabool, als je niet dichtbij `x = 0` zit.

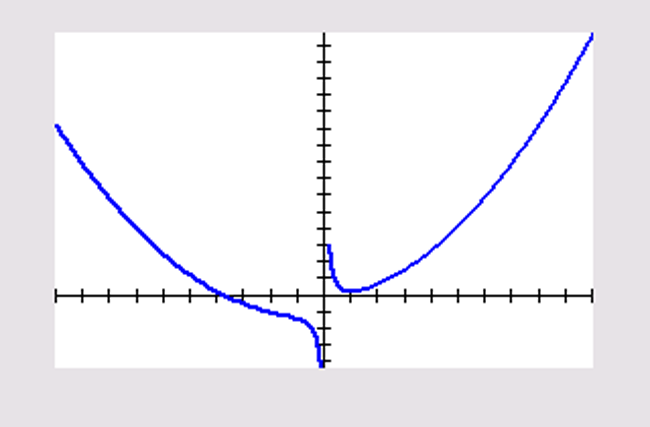
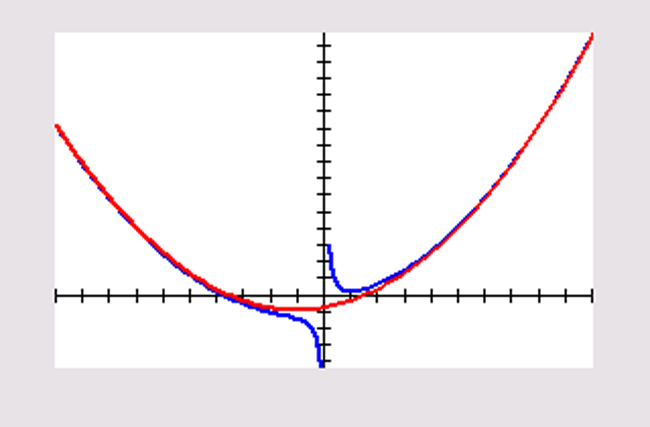
`f(x) = (x^3 + 2x^2 - 5x + 4)/x = x^2 + 2x - 5 + 4/x` .

`lim_(x rarr text(-)oo) (f(x) - (x^2 + 2x - 5)) = lim_(x rarr oo) 4/x = 0`

De vergelijking van de parabool is: `y = x^2 + 2x - 5` .

Met `C = 0,01` wordt de formule: `U = 12*(1-text(e)^(text(-)t/20))` .
`lim_(t rarr oo) 12*(1-text(e)^(text(-)t/20)) = 12*(1-0) = 12` , dus de limietspanning is `12` volt.

`12*(1-text(e)^(text(-)t/20)) = 0,9*12` geeft `text(e)^(text(-)t/20) = 0,1` en `t = text(-)20ln(0,1)~~46` s.

`f_5(x) = (2x(2x-5)+4)/(2x-5) = 2x + 4/(2x-5)`

`lim_(x → oo) (2x + 4/(2x-5) - 2x) = 0`

De vergelijking van de schuine asymptoot is `y = 2x` .

Als hoek `alpha` de hoek is die de schuine asymptoot met de positieve `x` -as maakt dan geldt `tan(alpha) = 2` dus `alpha~~63^@` .

Omdat de positieve `x` -as en iedere verticale lijn loodrecht op elkaar staan, geldt `beta = 90^@-alpha~~27^@` .

`f'_a(x) = ((8x-10)(2x-a)-(4x^2-10x+4)*2)/((2x-a)^2)`

`f'_a(x) = 0` geeft `8x^2 - 8ax + 10a - 8 = 0` en `x = (8a +- sqrt(64a^2 - 320a + 256))/16` .

Linker top op de `x` -as geeft `8a - sqrt(64a^2-320a+256) = 0` .

En hieruit volgt `64a^2 - 320a + 256 = 64a^2` en dus `a = 4/5` .

`4x^2 - 10x + 4 = 0` moet dezelfde oplossing hebben als `2x - a = 0` .

Met de abc-formule vind je: `x = 1/2 vv x = 2` .

`x = 1/2` geeft `a = 1` en `x = 2` geeft `a = 4` .

De grootste waarde van `a` is `4` .

`f_4(x) = (4x^2-10x+4)/(2x-4) = (4(x - 2)(x - 0,5))/(2(x-2)) = 2x-1` voor `x != 2` .

`lim_(x↑2) f_4(x) = lim_(x↓2) f_4(x) = 2*2-1 = 3`

De coördinaten van de perforatie zijn `(2, 3)` .

`y = 5` is de horizontale asymptoot, `x = 2` is de verticale asymptoot en `x = 0` is een perforatie.

`y = 0` is de horizontale asymptoot.

`x = 0` is de verticale asymptoot.

De vergelijking van de scheve asymptoot is `y = 2x+3` .

De vergelijking van de scheve asymptoot is `y = 4x` .