Voor `x!=0` is de functie te schrijven als:
`f(x) = 5/(x+5)`
Er geldt:
`lim_(x rarr oo) 5/(x+5) = lim_(x rarr text(-)oo) 5/(x+5) = 0`
`lim_(x uarr text(-)5) 5/(x+5) = text(-)oo` en `lim_(x darr text(-)5) 5/(x+5) = oo`
De functie heeft dus een horizontale asymptoot `y = 0` en een verticale asymptoot op `x = text(-)5` .
Verder geldt:
`lim_(x uarr 0) 5/(x+5) = lim_(x darr 0) 5/(x+5) = 1`
De functie heeft dus een perforatie op `(0, 1)` .

De functie heeft verticale asymptoten wanneer `x^2 - 4 = 0` :
`x = text(-)2 vv x = 2`
Er geldt:
`lim_(x uarr text(-)2) g(x) = lim_(x darr 2) g(x) = text(-)oo`
`g` heeft geen horizontale asymptoot.

De functie is ongedefinieerd wanneer `sin^2(x) = 0` , ofwel wanneer `sin(x) = 0` .
Dit geldt voor `x = kpi` .
`lim_(x uarr kpi) h(x) = lim_(x darr kpi) h(x) = oo`
De gevonden waarden zijn dus verticale asymptoten.

Er geldt:
`lim_(x rarr oo) (1/(x+4) - 1/(x+5)) = lim_(x rarr text(-)oo) (1/(x+4) - 1/(x+5)) = 0`
`lim_(x uarr text(-)5) (1/(x+4) - 1/(x+5)) = lim_(x darr text(-)4) (1/(x+4) - 1/(x+5)) = oo`
`lim_(x darr text(-)5) (1/(x+4) - 1/(x+5)) = lim_(x uarr text(-)4) (1/(x+4) - 1/(x+5)) = text(-)oo`
De functie `k` heeft dus een horizontale asymptoot `y = 0` en twee verticale asymptoten `x = text(-)4` en `x = text(-)5` .

Bekijk de grafiek op je GR. De functie lijkt lijnsymmetrisch ten opzichte van `x = 1` .

`f(1-p) = text(e)^(text(-)(1-1+p)^2) = text(e)^(text(-)p^2)`

`f(1+p) = text(e)^(text(-)(1-1-p)^2) = text(e)^(text(-)p^2)`

`f(1-p) = f(1+p)` voor willekeurige `p` , dus `f` is lijnsymmetrisch in `x = 1` .

Het functievoorschrift kan herleid worden: `(ln(x^2-2x+2))/(x-1) + 2 = (ln((x-1)^2+1))/(x-1) + 2` .
De functie lijkt puntsymmetrisch ten opzichte van `(1, 2)` .

`g(1-p) = ln((1-p-1)^2+1)/(1-p-1)+2 = text(-)ln(p^2+1)/p+2`

`g(1+p) = ln((1+p-1)^2+1)/(1+p-1)+2 = ln(p^2+1)/p+2`

Dus `(g(1-p)+g(1+p))/2 = 4/2 = 2` voor willekeurige `p` , dus `g` is puntsymmetrisch in `(1, 2)` .

De functie heeft verticale asymptoten wanneer `cos(x) = 0` , en lijkt lijnsymmetrisch ten opzichte van bijvoorbeeld `x = pi/2` .

`h(pi/2 - p) = (sin(pi/2 - p) + 1)/(cos^2(pi/2 - p)) = (sin(pi/2 + p) + 1)/(cos^2(pi/2 + p))`

`h(pi/2 + p) = (sin(pi/2 + p) + 1)/(cos^2(pi/2 + p))`

`h(pi/2 - p) = h(pi/2 + p)` voor willekeurige `p` , dus `h` is lijnsymmetrisch in `x = pi/2` .

Herleid: `f(x) = ((x-3)(x+1))/(x-2) = (x^2-2x-3)/(x-2) = x - 3/(x-2)` .

`lim_(x rarr text(-)oo) f(x) - x = lim_(x rarr oo)f(x) - x = 0`
De functie heeft dus een scheve asymptoot met vergelijking `y = x` .

`f` heeft een verticale asymptoot op `x = 2` . Als `f` puntsymmetrisch is, ligt het symmetriepunt op het snijpunt van de twee asymptoten, ofwel `(2, 2)` .

`f(2-p) = 2 - p - 3/(2-p-2) = 2 - p + 3/p`

`f(2+p) = 2 + p - 3/(2+p-2) = 2 + p - 3/p`

Dus `(f(2-p) + f(2+p))/2 = (2-p+3/p+2+p-3/p)/2 = 2` en voor willekeurige `p` is `(2, 2)` een symmetriepunt van `f` .

Noem het snijpunt van functie `f` en functie `g` punt `P` met `x_P=p` . Dan geldt:
`f(p) = g_k(p)` en `f'(p) = text(-)1/(g_k'(p))`

Dit oplossen geeft `k~~text(-)0,53 vv k~~3,13` .

`I = 1/3 pi*7^2(3*5 - 7) = 130 2/3 pi` cm³.

Voer in op de GR: `y_1 = 1/3 pi x^2(15 - x)` en `y_2 = 400` .
Venster bijvoorbeeld `[0, 10]xx[0, 500]` .
Je vindt: `h ~~ 6,84` cm.

`I = 1/3 pi (2r)^2(3r - 2r) = 4/3 pi r^3`

Er moet gelden `I = 1/32 * 4/3 pi r^3` .

Noem `h = a*r` , waarbij `0 le a le 2` en `r gt 0` .

Dit geeft `1/3 pi(ar)^2(3r - ar) = 1/24 pi r^3` en `a^2 - 1/3 a^3 = 1/24` .

Voer in op de GR: `y_1 = x^2 - 1/3 x^3` en `y_2 = 1/24` .
Venster bijvoorbeeld `[0, 1/12]xx[0, 2]` .
Je vindt: `x~~0,21` .

De hoogte van het waterpeil ten opzichte van de onderkant van de bal is `h~~0,21r` .

De hoogte van een trapeziumvormig zijvlak is `sqrt(h^2 + (1/6 a)^2) = sqrt(h^2 + 1/36 a^2)` .
De oppervlakte van een trapezium is dus: `1/2*a*sqrt(h^2 + 1/36 a^2) + 1/2*b*sqrt(h^2 + 1/36 a^2)`

Dit herleid je tot `1 1/6 a sqrt(h^2 + 1/36 a^2)`

De oppervlakte van de prullenbak is dus: `A = 4 * 1 1/6 a sqrt(h^2 + 1/36a^2) + a^2 = 4 2/3 a sqrt(h^2 + 1/36 a^2) + a^2` .

Gegeven is dat de inhoud gelijk is aan `30` L `=30000` cm³: `I = 30000` .

Tevens geldt `b = 1 1/3 a` . Invullen in de formule voor `I` geeft:

`30000 = 1/6 h(a^2 + 49/9 a^2 + 16/9 a^2)` en `30000 = 37/27 h a^2` , zodat `h = 810000/(37a^2)` .

Invullen in de formule voor `A` geeft: `A = 4 2/3 a sqrt((810000/(37a^2))^2 + 1/36 a^2) + a^2` .

GR: `a~~34,2` cm.

snelheid: `v(t) = text(-)lambda u text(e)^(text(-)lambda t)cos(omega t) - omega u text(e)^(text(-)lambda t)sin(omega t)`

versnelling: `a(t) = (lambda^2 - omega^2)u text(e)^(text(-)lambda t)cos(omega t) + 2lambda omega u text(e)^(text(-)lambda t)sin(omega t)`

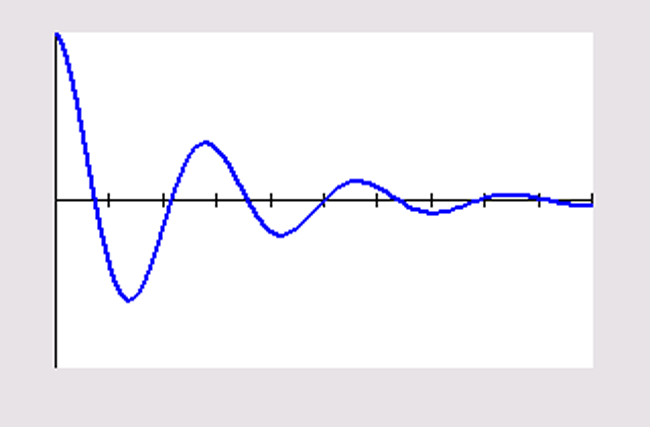
`v(0) = text(-)3/16`
`a(0) = text(-)2 23/64`

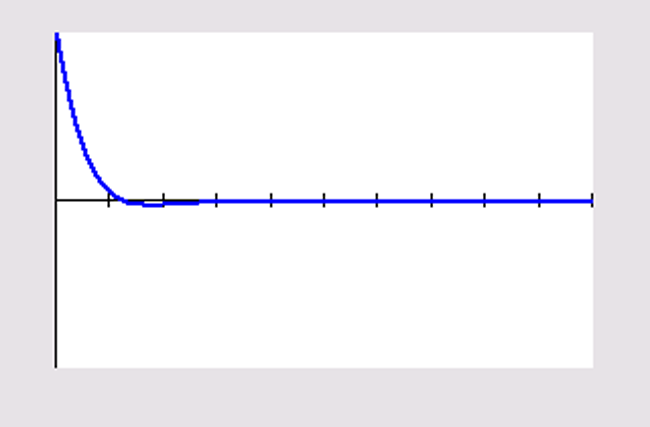
Je ziet dat de afwijking van het evenwichtspunt vrijwel zonder te trillen naar nul gaat. De dempingscoëfficiënt is in dermate groot dat de trilling meteen wordt afgeremd.

Er geldt `f(p) = ln(p^2 + 1)` en `g(p) = ln(text(e)^2/(p^2 + 1))` .

`AP = f(p)-1 = ln(p^2 + 1) - 1 = ln(p^2 + 1) - ln(text(e)) = ln((p^2 + 1)/(text(e)))`

`BP = 1 - g(p) = 1 - ln(text(e)^2/(p^2 + 1)) = ln(text(e)) + ln((p^2 + 1)/(text(e)^2)) = ln((p^2 + 1)/(text(e)))`

Dus `AP = BP` .

De inhoud van het omwentelingslichaam is gelijk aan tweemaal de inhoud van het omwentelingslichaam tussen de grafiek van `f` , de `y` -as, en de lijn `y=1` , omdat de grafieken van `f` en `g` gespiegeld zijn in die lijn:

`int_(f(0))^1 pi*(f^text(inv)(y))^2 text(d)y + int_1^(g(0)) pi*(g^text(inv)(y))^2 text(d)y = 2*int_(f(0))^1 pi*(f^text(inv)(y))^2 text(d)y`

Er geldt `f(0) = 0` . De inverse van `f` bepaal je door `x = f(y)` te herleiden voor `y` : `x = ln(y^2 + 1)` geeft `text(e)^x = y^2 + 1` en `y = sqrt(text(e)^x - 1)` .

Dus `f^(text(inv)) (y) = sqrt(text(e)^y - 1)` . De inhoud van het omwentelingslichaam is dus: `2*int_0^1 pi*(sqrt(text(e)^y - 1))^2 text(d)y = 2pi*int_0^1 (text(e)^y - 1) text(d)y = 2pi*[text(e)^y - y]_0^1 = 2pi*(text(e) - 2)` .

Bij de verschoven grafiek hoort het functievoorschrift `h(x) = f(x - 2) = ln((x-2)^2 + 1)`

Snijpunt bepalen: `ln(x^2 + 1) = ln((x-2)^2 + 1)` geeft `x^2 = (x-2)^2` en `x = 1` , dus het snijpunt is `(1, ln(2))` .

`f'(x) = (2x)/(x^2 + 1)` geeft `f'(1) = 1` .

`h'(x) = (2(x - 2))/((x - 2)^2 + 1)` geeft `h'(1) = text(-)1` .

Nu geldt `f'(1) * h'(1) = 1 * text(-)1 = text(-)1` en dus staan beide grafieken loodrecht op elkaar in het snijpunt.

`S = 58` geeft `a~~ 0,409`
`S = 63` geeft `a ~~ 0,134`
`0,13 ≤ a ≤ 0,41`

`a = 0,15` geeft `S ~~ 65` .
Voor grote waarden van `a` nadert `S` tot `58,82` .
Dus `59 ≤ S ≤ 65` .

De lengte van het ei is het verschil tussen de snijpunten van de grafiek van `f` met de `x` -as. Los dus op `f(x) = 0` :

`87x - 3x^2 - 2x^3 = x(87 - 3x - 2x^2) = 0` geeft `x = 0 vv x = (3+-sqrt((text(-)3)^2-4*text(-)2*87))/(text(-)4)`

De lengte van het ei is afgerond `5,89` cm.

`int_0^(5,9) pi(f(x))^2 text(d)x = ` `int_0^(5,9) pi*1/36(87x - 3x^2 - 2x^3) text(d)x = pi/36*[87/2x^2 - x^3 - 1/2 x^4]_0^(5,9) ~~ 61` cm³.

`f(4,3)~~2,11`
Dat wil zeggen dat de straal van een ronde opening ongeveer `2,11` cm is. Je zoekt de andere waarde van `x` waarvoor geldt `f(x) = 2,11` .
Voer in op de GR:
`y_1 = 1/6 sqrt(87x - 3x^2 - 2x^3)` en `y_2 = 2,11`
De optie intersect geeft `x~~2,3` .
Het ei is ongeveer `5,9` cm hoog, dus hij steekt ongeveer `5,9-2,3 = 3,6` cm boven het rekje uit.