Voorbeeld 1
Een parameterkromme is gegeven door
.
Breng deze kromme in beeld op de grafische rekenmachine.
Leg uit waarom dit een eenparige cirkelbeweging betreft en bereken de snelheid waarmee een punt van deze kromme beweegt.

|
|
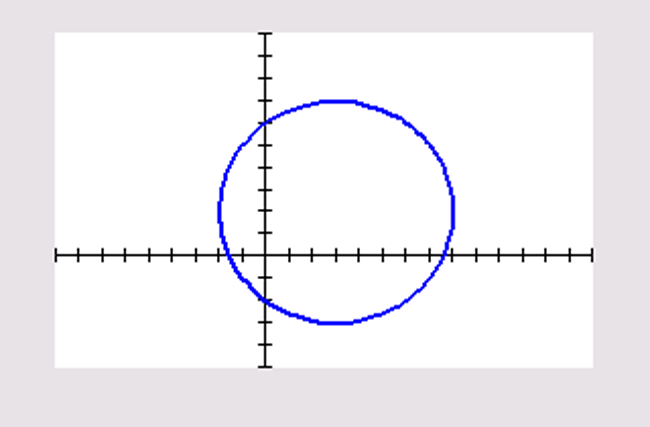
In het Practicum zie je hoe je met de grafische rekenmachine parameterkrommen in beeld kunt brengen. Hiernaast zie je de kromme.
Omdat een sinusoïde is met evenwichtsstand en amplitude geldt: .
Omdat een sinusoïde is met evenwichtsstand en amplitude geldt: .
Dit bepaalt je vensterinstellingen. Je lijkt een cirkel met middelpunt en straal te krijgen.
De periode van beide functies is , dus de cirkel wordt in seconden doorlopen.
De hoeksnelheid van
`vec(MP)`
is rad/s.
De snelheid waarmee beweegt is keer zo groot, dus eenheden/s.
De kromme is inderdaad een cirkel met middelpunt en straal als de afstand van elk punt op de cirkel tot gelijk is aan . Met de stelling van Pythagoras toon je aan dat dit voor elke klopt.
Bekijk Voorbeeld 1. Gegeven is nu een parameterkromme door `P(x(t),y(t)) = (1 + 6 cos((2pi)/15 * t), 2 + 6 sin((2pi)/15 * t))` .
Breng deze parameterkromme op je grafische rekenmachine volledig in beeld. Welk interval moet je dan voor de parameter `t` kiezen?
Waarom krijg je dezelfde kromme als je voor `t` waarden kiest vanaf `text(-)15` tot `40` ?
Wat krijg je voor figuur als je voor `t` waarden kiest vanaf `0` tot `8` ?
Je kunt ook de stapgrootte van `t` instellen. Wat gebeurt er als je die op `1` instelt, te beginnen bij `t = 0` ?
Bekijk Voorbeeld 1. Er wordt beweerd dat `P` over een cirkel met middelpunt `M(3, 2)` loopt.
Bewijs dit met behulp van de stelling van Pythagoras. Aan welke vergelijking in `x` en `y` voldoet elk punt van deze kromme?
Maak op je rekenmachine de parameterkromme waarvoor geldt
`(x, y) = (3 + 5sin((2π)/10 * t), 2 + 5cos((2π)/10 * t))`
.
Krijg je dezelfde kromme als in het voorbeeld of zijn er verschillen? En zo ja, wat zijn die verschillen?