`f'(x) = 2^x ln(2)` , `f''(x) = 2^x ln^2(2)` , `f^((3)) (x) = 2^x ln^3(2)` , enz...

`f^((n)) (x) = 2^x ln^n(2)`

Gebruik `2^0 = 1` .

`f'(0) = ln(2)` , `f''(0) = ln^2(2)` , `f^((3)) (0) = ln^3(2)` , enz...

`f(x) ~~ 1 + x ln(2) + 1/2 x^2 ln^2(2) + 1/6 x^3 ln^3(2) + 1/24 x^4 ln^4(2) + 1/120 x^5 ln^5(2)` .

Vergelijk beide grafieken. De benadering wordt beter als je de Taylorbenadering verder voortzet.

`f'(x) = (text(-)1)/(x^2)` , `f''(x) = (2)/(x^3)` , `f^((3)) (x) = (text(-)6)/(x^4)` , enz...

`f^((n)) (x) = (text(-)1)^n*((n)!)/(x^(n+1))`

Je kunt `x = 0` niet invullen in de functie en zijn afgeleiden.
De functie is niet differentieerbaar voor `x=0` .

Binair delen lukt wel, zie voorgaande paragraaf.

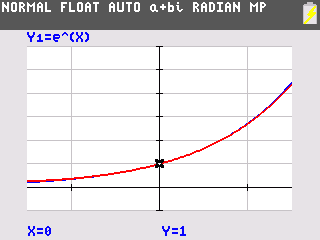
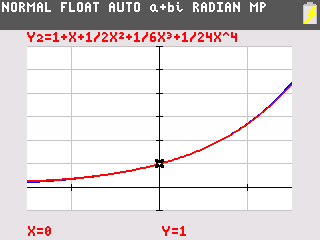
Vergelijk beide grafieken, zie de figuren.

`text(e)^x ~~ 1 + x + 1/2 x^2 + 1/6 x^3 + 1/24 x^4 + 1/120 x^5 + 1/720 x^6`

Grafische rekenmachine (afhankelijk van het merk): `text(e) = text(e)^1 ~~ 2,718281828` .

Met de vijfterm: `text(e)^1 ~~ 1 + 1 + 1/2 + 1/6 + 1/24 ~~ 2,708333333` .

Met de zeventerm: `text(e)^1 ~~ 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + 1/720 ~~ 2,718055556` .

Dit hangt nogal af van je grafische rekenmachine.
Stel hij geeft `text(e) = text(e)^1 ~~ 2,718281828` (dit wordt geen herhaling!).
Een tienterm geeft dan `text(e)^1 ~~ 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + 1/720 + 1/5040 + 1/40320 + 1/362880 ~~ 2,718281526` .
Pas bij `13` termen vind je dezelfde waarde als deze rekenmachine opgeeft.

Deze functie is niet differentieerbaar voor `x = 0` .

Deze functie is wel differentieerbaar voor `x = 0` .

`g'(x) = 1/(x+1)` , `g''(x) = (text(-)1)/((x+1)^2)` , `g^((3))(x) = (2)/((x+1)^3)` , `g^((4))(x) = (text(-)6)/((x+1)^4)` en `g^((5))(x) = (24)/((x+1)^5)` .

Dus `g(x) = ln(x+1) ~~ x - 1/2 x^2 + 1/3 x^3 - 1/4 x^4 + 1/5 x^5` .

`ln(x) ~~ x - 1 - 1/2 (x-1)^2 + 1/3 (x-1)^3 - 1/4 (x-1)^4 + 1/5 (x-1)^5` .

Vergelijk de grafieken van `y_1=ln(x)` en `y_2 = x - 1 - 1/2 (x-1)^2 + 1/3 (x-1)^3 - 1/4 (x-1)^4 + 1/5 (x-1)^5` (in de buurt van `x=0` ).

`f'(x) = cos(x)` , `f''(x) = text(-)sin(x)` , `f^((3))(x) = text(-)cos(x)` , `f^((4))(x) = sin(x)` , `f^((5))(x) = cos(x)` .

Gebruik `sin(0) = 0` , `cos(0) = 1` . (Denk om radialen!)

`f(x) = sin(x) = x - 1/6 x^3 + 1/120 x^5 - 1/5040 x^7 + 1/362880 x^9 - 1/3991680 x^11`

`sin(1/2 pi) ~~ 0,9731965473` , dus mwah!

`sin(1/4 pi) = 1/2 sqrt(2) ~~ 0,7071067812` .

Taylorbenadering met vier termen: `sin(1/4 pi) ~~ 0,7071064696` .
Dus een benadering met vier termen is genoeg om zes decimalen nauwkeurig te krijgen.

`sin(1^@) = sin(1/180 pi) ~~ 0,0174524064` (Taylorbenadering met vier termen).

`f(x) = cos(x) = 1 - 1/2 x^2 + 1/24 x^4 - 1/720 x^6 + 1/40320 x^8 - ...` .

`cos(x) = sin(1/2 pi - x) = sin(x + 1/2 pi)` , dus de cos-functie is een verschoven sin-functie.

Nee, immers `tan(x) = (sin(x))/(cos(x))` , dus dit kan met binair rekenen worden opgelost vanuit Taylorbenaderingen van `sin(x)` en `cos(x)` .

Gebruik `\ ^2log(x) = (ln(x))/(ln(2))` .

Eerder: `ln(x) ~~ x - 1 - 1/2 (x-1)^2 + 1/3 (x-1)^3 - 1/4 (x-1)^4 + 1/5 (x-1)^5 - ...` .

Dus: `\ ^2log(x) ~~ 1/(ln(2))(x - 1 - 1/2 (x-1)^2 + 1/3 (x-1)^3 - 1/4 (x-1)^4 + 1/5 (x-1)^5 - ...)` .

Nu is `x = 1/2` en dus `x-1= text(-)1/2` .
Voer dit in de Taylorbenadering in die je bij a hebt gevonden.
Je krijgt `\ ^2log(1/2) ~~ text(-)0,99335...` en dat wijkt `0,00665...` af van de juiste uitkomst.

`f(x) = 1/(1+x) = 1 - x + x^2 - x^3 + x^4 - x^5 + ...`

Taylorbenadering met drie termen: `f(0,0034) ≈ 0,99661156` .
Grafische rekenmachine: `f(0,0034) ≈ 0,9966115208` .
Met drie termen heb je al een benadering in zes decimalen nauwkeurig.

`E(v) = m_0 c^2 (1 - 1/(c^2) * v^2 )^(text(-)1/2)` en dan hogere afgeleiden berekenen.
Je krijgt: `E(v) ~~ m_0 c^2 + 1/2 m_0 v^2 + (3m_0)/(8c^2) v^4` .

De eerste term is de rustenergie en de tweede term is de bewegingsenergie van de massa.

Uit `arcsin(sin(x)) = x` volgt na beide zijden differentiëren: `[arcsin(sin(x))]' * cos(x)=1` .
Dit geeft `[arcsin(sin(x))]' = 1/(cos(x)) = 1/(sqrt(1-sin^2(x)))` .
Vervang nu `sin(x)` door `x` en je krijgt: `[arcsin(x)]' = 1/(sqrt(1 - x^2))` .

`arcsin(x) = x + 1/2 * (x^3)/(3) + (1*3)/(2*4) * (x^5)/(5) + (1*3*5)/(2*4*6) * (x^7)/(7) + ...`

`pi = 6 * arcsin(1/2) ≈ 3,14115534` als je de Taylorbenadering met vier termen bij b gebruikt.

GR: `text(e)^2 ~~ 7,389056099`

Taylorbenadering: `text(e)^2 ~~ 1 + 2 + 1/2 * 2^2 + 1/6 * 2^3 + 1/24 * 2^4 = 7`

En daarna: `text(e)^2 ~~ 1 + 2 + 1/2 * 2^2 + 1/6 * 2^3 + 1/24 * 2^4 + 1/120 * 2^5 = 7,2666...`

En daarna: `text(e)^2 ~~ 1 + 2 + 1/2 * 2^2 + 1/6 * 2^3 + 1/24 * 2^4 + 1/120 * 2^5 + 1/720 * 2^6 = 7,3555...`

Enzovoort...

`text(e)^x ~~ text(e)^2(1 + x + 1/2 x^2 + 1/6 x^3 + 1/24 x^4 + ...)`

Benadering rond `x=0` geeft `text(e)^(2,1) ~~ 1 + 2,1 + 1/2 2,1^2 + 1/6 2,1^3 + 1/24 2,1^4 ~~ 7,6588375` .

Benadering rond `x=2` geeft `text(e)^(2,1) ~~ text(e)^2(1 + 0,1 + 1/2 0,1^2 + 1/6 0,1^3 + 1/24 0,1^4) ~~ 8,166169286` .

GR geeft `text(e)^(2,1) ~~ 8,166169913` . De tweede benadering is dus meteen veel beter.

`f'(x) = 1/(2sqrt(x))` en daarin kun je `x = 0` niet invullen.

`g(x) = sqrt(x+1) = 1 + 1/2 x - 1/8 x^2 + 3/16 x^3 - 5/128 x^4 + ...`

`sqrt(1,2) = g(0,2) ~~ 1,0964`