Antwoorden van de opgaven
Tussen `x = 1` en `x = 2` .
Tussen `x = 1,6` en `x = 1,7` .
Tussen `x = 1,63` en `x = 1,64` .
Tot vier decimalen.
`x ~~ 1,634`
Werk zoals in de Uitleg 1. Je vindt als het goed is weer `x ≈ 1,634` .
Los op
`v(x) = f(x)-g(x) = 4-x-x^2 = 0`
.
Nulpunt in
`[1, 2]`
dus
`x = (1+2)/2 = 1,5`
en
`v(1)*v(1,5) gt 0`
en
`v(1,5)*v(2) lt 0`
.
Nulpunt in
`[1,5; 2]`
dus
`x = (1,5+2)/2 = 1,75`
en
`v(1,5)*v(1,75) lt 0`
.
Nulpunt in
`[1,5; 1,75]`
dus
`x = (1,5+2)/2 = 1,625`
en
`v(1,5)*v(1,625) lt 0`
.
Nulpunt in
`[1,5; 1,625]`
dus
`x = 1,5625`
en
`v(1,5)*v(1,5625) lt 0`
.
Etcetera.
Je vindt
`x ≈ 1,56155`
.
Je moet ook op de GR het zoekgebied inklemmen: linkergrens en rechtergrens instellen.
Gebruik
`y_1 (x) = x^3 + x - 6`
en
`y_2 (x) = 3x^2 + 1`
.
Werk zoals in de GR-figuren in de uitleg staat:
`x ≈ 1,63436`
.
Neem
`y_1 = 6 - 2sqrt(x-3)`
en de afgeleide
`y_2 = (text(-)1)/(sqrt(x-3))`
en loop
`x_(n+1) = x_n - (y_1 (x_n))/(y_2 (x_n))`
na.
Begin b.v. met
`x_0 = 10`
.
Je krijgt
`x ≈ 12,00000000`
al na vier stappen.
De exacte uitkomst
`x = 12`
vind je natuurlijk algebraïsch.
`x^4 - 4x = 12 + x` geeft `x^4 - 5x - 12 = 0` .
Neem
`y_1 = x^4 - 5x - 12`
en de afgeleide
`y_2 = 4x^3 - 5`
en loop
`x_(n+1) = x_n-(y_1 (x_n))/(y_2 (x_n))`
na.
Begin b.v. met
`x_0 = 2`
voor het rechter snijpunt (nulpunt van
`y_1`
).
Je vindt al na drie stappen
`x ≈ 2,188578`
.
Voor het linker snijpunt start je b.v. met
`x_0 = text(-)2`
. En je vindt:
`x ≈ text(-)1,46889`
.
Ga na dat je dezelfde antwoorden krijgt als in het voorbeeld.
Nulpunt bepalen van `y_1 = x^3 - 17` .
Halveringsmethode:
in
`[2, 3]`
:
`x = 2,5`
en
`y_1 (2,5)*y_1 (3) lt 0`
in
`[2,5; 3]`
:
`x = 2,75`
en
`y_1 (2,5)*y_1 (2,75) lt 0`
in
`[2,5; 2,75]`
:
`x = 2,625`
en
`y_1 (2,5)*y_1 (2,625) lt 0`
in
`[2,5; 2,625]`
:
`x = 2,5625`
en
`y_1 (2,5625)*y_1 (2,625) lt 0`
etc.
Je vindt
`x ≈ 2,5712`
.
De N-R-methode:
Neem
`y_1 = x^3 - 17`
en de afgeleide
`y_2 = 3x^2`
en loop
`x_(n+1) = x_n - (y_1 (x_n))/(y_2 (x_n))`
na.
Start met b.v.
`x_0 = 3`
en je vindt:
`x ≈ 2,5712`
.
Maak eerst de grafiek van `f` met je GR en schat een goede interval waar het snijpunt binnen moet liggen.
Maak tabellen met steeds meer decimalen en je vindt `x ~~ 1,49612` .
Neem als startinterval bijvoorbeeld `[1, 2]` en pas de methode toe.
Je vindt weer `x ~~ 1,49612` .
Voer in je GR in `y_1 = x^5 - x - 6` en de afgeleide `y_2 = 5x^4 - 1` en loop `x_(n+1) = x_n - (y_1 (x_n))/(y_2 (x_n))` na.
Je vindt weer `x ~~ 1,49612` .
De N-R-methode is het snelst.
Neem `y_1 = x^2 - 3` en `y_2 = 2x` en de N-R-methode geeft `x ≈ 1,73205` .
Taylorbenadering:
`sqrt(x+1) = 1 + 1/2 x - 1/8 x^2 + 3/16 x^3 - 5/128 x^4 + 7/256 x^5 - ...`
.
Door
`x = 2`
invullen valt
`sqrt(3)`
echter niet te benaderen, want deze Taylorbenadering nadert niet naar een bepaalde waarde.
`y_1 = 4 - x - x^3` en `y_2 = text(-)1 - 3x^2` geeft met de N-R-methode: `x ≈ 1,378797` .
De halveringsmethode met begin het interval `[1, 2]` kan ook.
`y_1 = cos(x) - x` en `y_2 = text(-)sin(x) - 1` geeft met de N-R-methode: `x ≈ 0,739085` .
`y_1 = text(e)^(2x) + 4x - 8` en `y_2 = 2text(e)^(2x) + 4` geeft met de N-R-methode: `x ≈ 0,788908` .
`y_1 = x^4 - 4x - 6` en afgeleide `y_2 = 4 x^3 - 4` geeft met de N-R-methode: `x ~~ text(-)1,114412` en `x ~~ 1,923708` .
Je zou zoiets moeten krijgen:

|
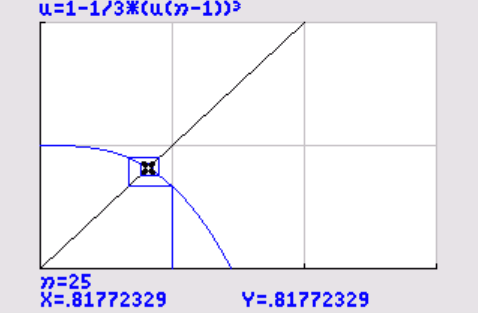
|
`x ≈ 0,8177`
Nu maak je
`x = 6-x^3`
en dus moet je de webgrafiek bij de rij
`u(n)=6 - (u(n-1))^3`
maken.
Je ziet dan de waarden steeds verder weglopen van het punt waar de grafiek van de rij en de lijn
`y=x`
elkaar snijden.
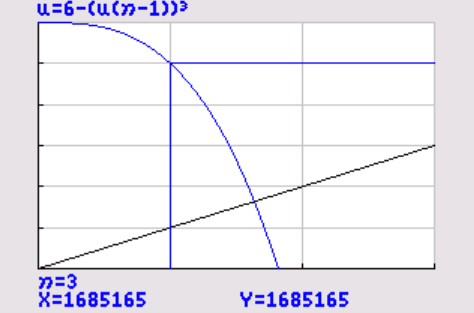
De helling van `y_1 = x` is `1` .
Omdat de helling van `y_2 = 6 - x^3` in het snijpunt met `y_1` kleiner is dan `text(-)1` loopt de grafiek van `y_2` daar in de buurt zo steil naar beneden dat de `y` -waarden steeds verder van die van het snijpunt af komen te liggen.
Je krijgt `x ~~ 2,46784` .