Een fabrikant van spelcomputers heeft ontdekt dat er een verband bestaat tussen de verkoopprijs `p` van een spelcomputer (€) en het aantal spelcomputers `q` dat per dag wordt verkocht.
Dit verband is: `q = 300 - 0,5p` .

De opbrengst `R` (€) per dag bereken je door het aantal verkochte spelcomputers te vermenigvuldigen met de verkoopprijs. De formule voor de opbrengst is: `R = q*p` .

Door deze twee formules met elkaar te combineren kun je een formule opstellen voor de opbrengst afhankelijk van de verkoopprijs.

Vul deze uitdrukking voor `q` nu in de formule `R = q*p` in:

`R = p*q = p * (300 - 0,5p) = 300p - 0,5p^2`

Er ontstaat een kwadratische formule.

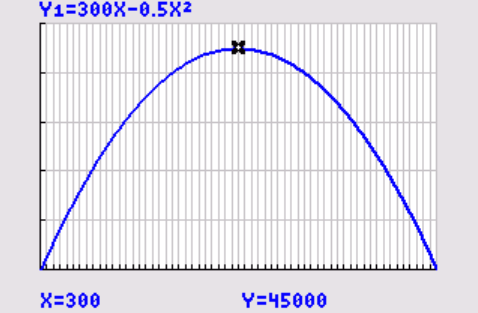
De bijbehorende grafiek is een bergparabool. De top van deze parabool geeft aan voor welk aantal verkochte spelcomputers per dag de opbrengst maximaal is.
Voer in je grafische rekenmachine in: `y_1 = 300x - 0,5x^2` met als venster bijvoorbeeld `0 le x le 600` en `0 le y le 50000` . Bepaal het maximum van de grafiek, dit geeft: `x = 300` en `y = 45000` .
Bij een verkoopprijs van € 300,00 per spelcomputer is de opbrengst per dag maximaal, de opbrengst is dan € 45000,00.

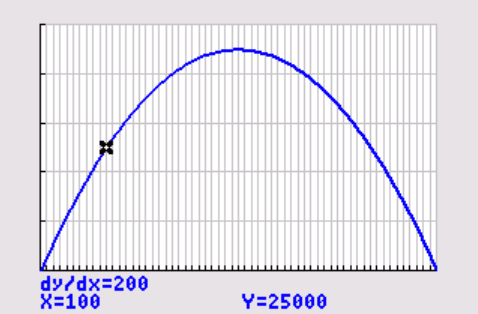
Het hellingsgetal van een punt `x` op de grafiek kun je vinden met de grafische rekenmachine. Je schrijft het als `(text(d)y)/(text(d)x)` . Het hellingsgetal voor `x = 100` is gelijk aan `200` . Uit de grafiek blijk dat het hellingsgetal in een punt links van de top positief is. Het hellingsgetal in een punt in een top is meestal `0` .