Antwoorden van de opgaven
Het is een rechte lijn. Gaat door de punten `(0, 0)` en `(10, 40)` ;
het hellingsgetal is: `(40-0)/(10-0) = 4` ;
het startgetal is: `0` .
de formule wordt: `v = 4t` .
Dat wordt een (halve) parabool:

`s = 2t^2` geeft `s(20) = 800` m.
Voer in je GR in Y1=X^2 en gebruik de optie dy/dx.
| `x` | `text(-)3` | `text(-)2` | `text(-)1` | `0` | `1` | `2` | `3` |
| `f'(x)` | `text(-)6` | `text(-)4` | `text(-)2` | `0` | `2` | `4` | `6` |
Vergelijk jouw grafiek met die in de uitleg.
De grafiek voldoet aan `y=2x` .
Voor de `x` -waarde die hoort bij `f'(x)=0` heeft de grafiek van `f` een horizontale raaklijn. Hier is dat voor `x = 0` .
| `x` | `text(-)3` | `text(-)2` | `text(-)1` | `0` | `1` | `2` | `3` |
| `f'(x)` | `7,5` | `0` | `text(-)4,5` | `text(-)6` | `text(-)4,5` | `0` | `7,5` |
Voer in Y1=0.5X^3-6X en Y2=(Y1(X+0.001)-Y1(X))/(0,001).
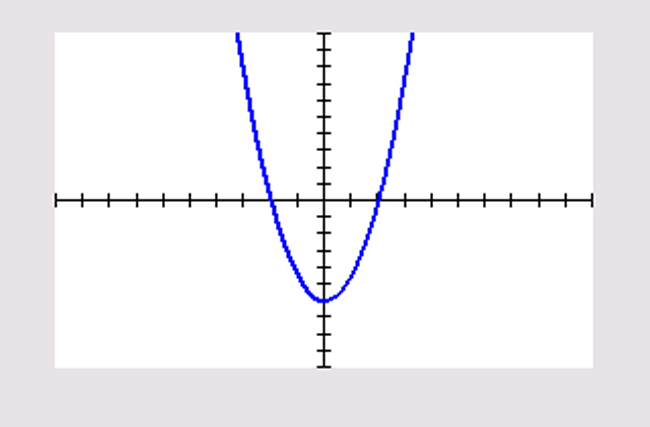
Bij een top van een grafiek hoort een raaklijn met hellingsgetal `0` .
`f'(1)=text(-)4,5` en `f(1)=text(-)5,5` dus de raaklijn wordt: `y=text(-)4,5 x-1` .
`f'` heeft een minimum van `text(-)6` voor `x = 0` . De grafiek van `f` gaat daar van toenemend dalend over naar afnemend dalend.
Wat betekent het voor de grafiek van de functie als de hellingsgrafiek onder de `x` -as ligt?
De functiewaarden zijn negatief.
De grafiek is stijgend.
De grafiek is dalend.
De grafiek heeft een minimum.
Soms is een grafiek toenemend stijgend. Hoe zie je dat aan de hellingsgrafiek?
De hellingsgrafiek ligt boven de `x` -as.
De hellingsgrafiek is stijgend.
De hellingsgrafiek ligt boven de `x` -as en is stijgend.
De hellingsgrafiek heeft een maximum.
Hoe vind je de extremen van een functie uit de hellingsgrafiek?
Je bekijkt voor welke waarden van `x` de hellingsgrafiek een maximum of een minimum heeft.
Je bekijkt voor welke waarden van `x` de helling overgaat van positief in negatief of omgekeerd.
Je bekijkt voor welke waarden van `x` de helling de waarde `0` heeft.
Dat kun je niet uit de hellingsgrafiek aflezen.
Kies uit de volgende antwoorden. De grafiek van `f` heeft:
precies één extreme waarde van `5` voor `x=0` ;
geen extremen want de hellingsgrafiek is dalend;
geen extremen want de grafiek van de functie zelf is ook dalend;
een maximum voor `x=3`
Grafiek B.
C
Voor
`x=0`
is de helling van de grafiek van
`f`
gelijk aan
`0`
.
Waarom heeft de grafiek van
`f`
geen extreme waarde voor
`x=0`
? (Geef alle goede antwoorden aan.)
De grafiek is altijd stijgend, behalve bij `x=0` .
Het tekenschema van de afgeleide wisselt bij `x=0` niet van teken.
De functie heeft geen horizontale raaklijn voor `x=0` .
De functie heeft wel een horizontale raaklijn voor `x=0` maar gaat niet van stijgend naar dalend.
Grafiek B.
| `x` | `text(-)3` | `text(-)2` | `text(-)1` | `0` | `1` | `2` | `3` |
| `g'(x)` | `text(-)6` | `text(-)4` | `text(-)2` | `0` | `2` | `4` | `6` |
Deze tabel past bij een lineaire functie met hellingsgetal `2` en begingetal `0` .
Dus `g'(x) = 2x` .
Met de GR via dy/dx:
`a'(5 )=12` m/s en dat is `12*3,6=43,2` km/h.
De grafiek van
`v(t)`
is de hellinggrafiek van
`a(t)`
.
Zo'n hellinggrafiek kun je met je GR tekenen. Voer in Y1=1.2*X^2 en Y2=(Y1(X+0.001)-Y1(X))/(0.001) en je krijgt een goede benadering ervan. De hellinggrafiek is een rechte lijn door
`(0 , 0)`
en
`(5 , 12)`
.
Van die rechte lijn is het hellingsgetal `(12-0)/(5-0) = 2,4` en het begingetal `0` .
De bijbehorende formule wordt: `v(t) = a'(t) = 2,4t` .
`50` km/h is omgerekend: `50/(3,6)~~13,89` m/s.
`v(t)=13,89` invullen: `2,4 t≈13,89` geeft `t≈5,8` seconden.
Na `5,8` seconden beweegt de zeilwagen met een snelheid van `50` km/h.
De blauwe grafiek (met de langere streepjes).
Bijvoorbeeld zo. De ligging van de grafiek ten opzichte van de `x` -as kun je niet weten, net zo min als de mate van stijging of daling.

Je ziet de hellingsgrafiek van `f` . De grafiek van `f` is stijgend als de hellingsgrafiek positief is (boven de `x` -as ligt), dus op het interval: `⟨text(-)1 , 1 ⟩` .
Voor extreme waarden geldt vaak `f'(x)=0` . Maar dit kunnen zowel minima als maxima zijn. Een maximum is te vinden als `f'(x)` van positief naar negatief gaat. Dit is het geval bij `x=1` .
Nee, daarvoor moet je het functievoorschrift van `f` weten.
Je grafiek moet in ieder geval door `(0 , 2)` gaan en een maximum hebben voor `x = 1` en een minimum voor `x=text(-)1` .
Voer in: Y1=0.5X^2+3X.
Gebruik
`(text(d)y)/(text(d)x)`
. Maak een tabel van de hellingsfunctie:
| `x` | `0` | `1` | `2 ` | `3 ` | `4` |
| `f'(x)` | `3` | `4 ` | `5` | `6` | `7` |
Lineaire functie met hellingsgetal `1` en begingetal `3` .
Functievoorschrift: `f'(x) = x + 3` .
Vul elke functie in de GR in en bepaal `(text(d)y)/(text(d)x)` als `x = 1` :
-
`f'(1) = text(-)2`
-
`g'(1) = 0,5`
-
`h'(1) = text(-)4`
-
`k'(1) = 0`
Vul elke functie als Y1 in de GR in en neem Y2=(Y1(X+0.001)-Y1(X))/(0.001).
Bij de extremen van de gekozen functie zit een nulpunt bij de hellingsfunctie van die grafiek, want de helling in een top is `0` . Bepaal de nulpunten van de hellingsgrafiek:
`f(x)` : `x = 0` , max. `f(0) = text(-)(0^2) + 4 = 4` ;
`g(x)` : `x = 0` , max. `g(0) = sqrt(0^2+3) = sqrt(3)` ;
`h(x)` : geen nulpunten, geen extremen;
`k(x)` : `x = 1` , max. `k(1) = text(-)1^4 + 4*1 = 3` .
Voer in: Y1=2X^3-6X^2-8X.
Venster bijvoorbeeld:
`text(-)2 le x le 5`
en
`text(-)30 le y le 10`
.
Bereken met de GR het snijpunt van de grafiek met de
`x`
-as.
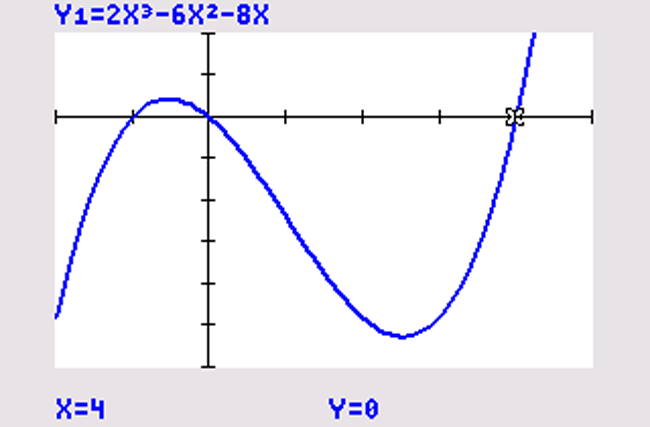
Met de GR: gebruik dy/dx.

Het hellingsgetal bij dit punt is `40` .
Een raaklijn is een rechte lijn. Je zoekt de richtingscoëfficiënt `a` en het begingetal `b` .
De richtingscoëfficiënt is gelijk aan het hellingsgetal: `40` .
De lijn gaat in ieder geval door het punt `(4, 0)` .
De vergelijking van de raaklijn aan `f(x)` door `(4, 0)` is dan: `y = 40x - 160` .
Voer in: Y1=2X^3-6X^2-8X en Y2=(Y1(X+0.001)-Y1(x))/(0.001).
Venster bijvoorbeeld:
`text(-)2 le x le 5`
en
`text(-)30 le y le 10`
.
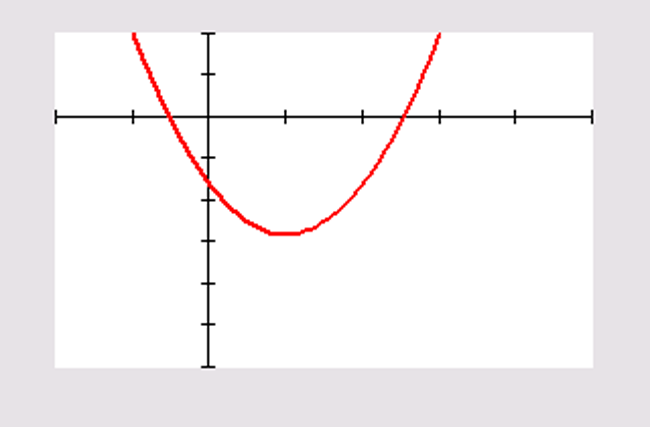
Nulpunten van de hellingsgrafiek bepalen en de gevonden
`x`
-waarden invullen in
`f`
.
Je vindt: min.
`f(2,53) ≈ text(-)26,26`
en max.
`f(text(-)0,53) ≈ 2,26`
.
De afgelegde weg wordt in meters uitgedrukt. De hellingsgrafiek geeft de verandering per seconde. De hellingsgrafiek wordt dus uitgedrukt in m/s.
Voer in: Y1=1.6X^2 en Y2=(Y1(X+0.001)-Y1(X))/(0.001) en je ziet (een benadering van) de hellingsgrafiek.
De richtingscoëfficiënt van de lijn blijkt `3,2` en het begingetal is `0` , dus `v(t) = 3,2t` .
`v` wordt uitgedrukt in m/s. Reken eerst de `80` km/h om: `80/(3,6) ~~ 22,22` m/s.
Invullen in de formule levert:
`22,22 = 3,2t` en dus `t = (22,22)/(3,2) ~~ 6,94` .
Na ongeveer `7` s is de snelheid meer dan `80` km/h.
-
Grafiek 4 hoort bij model A want de helling is constant hetzelfde.
-
Grafiek 1 hoort bij model B want de helling neemt voortdurend af.
-
Grafiek 3 hoort bij model C want de helling neemt eerst toe en dan af maar blijft positief.
-
Grafiek 2 hoort bij model D want de helling neemt eerst toe en dan af en wordt negatief.
(bron: examen vwo wiskunde A in 2002, tweede tijdvak)
Je vindt de grafiek van: `f'(x) = 2x - 4` .
De grafiek van `g` moet in ieder geval door het punt `(2 , 4 )` gaan en drie extremen hebben: maxima voor `x = text(-)3` en `x = 3` en een minimum voor `x=0` .
Voor `x=0` .
Op het interval `(:0 , 3 :)` .
De grafiek van `f` moet in ieder geval door `(0 , 1)` gaan en twee extremen hebben: een maximum voor `x = 0` (zie a) en een minimum voor `x = 3` .