Verwerken
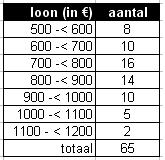
Bekijk de frequentieverdeling van de weeklonen van `65` werknemers van een bedrijf.
Geef de ondergrens van de zesde klasse.
Geef de bovengrens van de vierde klasse.
Geef het klassenmidden van de derde klasse.
Welke ondergrens en welke bovengrens heeft de vijfde klasse?
Welke klassenbreedte is hier gebruikt?
Is hier sprake van relatieve of van absolute frequenties?
Voor een toets kun je maximaal
`100`
punten scoren. Je ziet hoe een groep van veertig personen de toets heeft gemaakt:
59 – 57 – 53 – 60 – 63 – 58 – 77 – 33 – 50 – 59
58 – 75 – 62 – 54 – 53 – 78 – 59 – 68 – 65 – 62
57 – 60 – 80 – 47 – 90 – 30 – 60 – 35 – 57 – 87
63 – 65 – 63 – 58 – 65 – 70 – 73 – 58 – 63 – 55
Deel deze scores in klassen in. Neem als laagste klasse `25- lt 35` . Maak een frequentietabel.
Maak bij deze tabel een kolom van relatieve frequenties.
Genereer in Excel of met de grafische rekenmachine honderd toevalsgetallen van `1` tot en met `20` .
Maak een turftabel.
Maak een frequentietabel.
Maak een tabel met relatieve frequenties en somfrequenties.
Welke relatieve frequenties verwacht je bij de twintig getallen als je `10^6` toevalsgetallen van `1` tot en met `20` zou genereren?
Bekijk de klassenindeling met de lengtes van zestig jongens.
| lengte (cm) | abs. freq. | rel. freq. | cum. rel. freq. (%) |
| `150 - lt 165` | `15` | `0,25` | `25` |
| `165 - lt 175` | `15` | `0,25` | `50` |
| `175 - lt 180` | `15` | `0,25` | `75` |
| `180 - lt 185` | `5` | `0,083` | `83,3` |
| `185 - lt 190` | `5` | `0,083` | `91,7` |
| `190 - lt 195` | `5` | `0,083` | `100` |
| totaal | `60` | `1` | `100` |
Waarom voldoet deze klassenindeling niet aan de regels?
Wat valt je op aan deze klassenindeling?
Leg uit waarom dergelijke klassenindelingen niet goed bruikbaar zijn.
Maak met de gegevens uit de tabel een geschikte klassenindeling. Bepaal nu de frequentie, de relatieve frequentie en de cumulatieve relatieve frequentie.
Klopt je antwoord op b nog steeds? Zo niet, wat geeft de tabel nu voor indruk?
Bekijk de frequentietabellen met weeklonen van twee bedrijven. Alle werknemers zijn opgenomen in de tabellen.
Bedrijf 1 |
Bedrijf 2 |
Noem twee redenen waarom je de weeklonen van deze twee bedrijven niet zinvol met elkaar kunt vergelijken als je alleen naar deze frequentietabellen kijkt.
Maak frequentietabellen waarmee je de weeklonen van deze twee bedrijven wel goed kunt vergelijken.
Een van de onderzoeksvragen is: "In welk bedrijf zijn er relatief meer mensen die minder dan € 600,00 per week verdienen?"
Uit welk soort frequentietabel zou je dit direct kunnen aflezen? Geef een antwoord op deze onderzoeksvraag.
Het is niet mogelijk om de percentages werknemers die minder dan € 650,00 per week verdienen met elkaar te vergelijken. Leg uit waarom dat niet kan en bedenk een manier om daar wel een schatting van te kunnen maken.