Voorbeeld 3
In het leeftijdsdiagram van de Nederlandse bevolking in 2000 zie je hoe de klassenindeling `0-9` , `10-19` , `20-29` , enzovoort wordt gebruikt. De aantallen Nederlanders zijn duizendtallen. Bijvoorbeeld de klasse `10-19` bevat de Nederlandse mannen of vrouwen die een leeftijd hebben vanaf `10` tot `20` jaar.
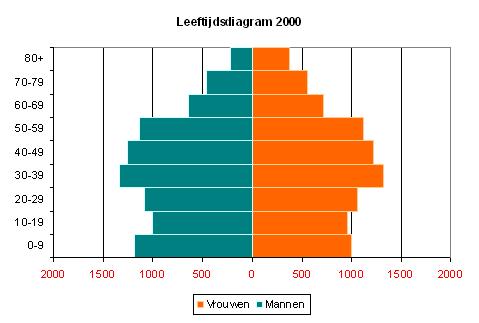
Kun je met de gegevens in dit diagram een nieuw leeftijdsdiagram maken met klassen van `0 - 14` , `15 - 29` , `30 - 44` , enzovoort? En met klassen van `0 - 19` , `20 - 39` , enzovoort? Licht je antwoord toe.
Omdat in de klasse
`0 - 14`
de klasse
`0 - 9`
geheel en de klasse
`10 - 19`
voor een deel is opgenomen, kun je uit dit diagram niet opmaken hoeveel Nederlanders in de klasse
`0 - 14`
moeten komen. Je kent de onderverdeling van de klassen namelijk niet. Je weet alleen het totale aantal Nederlanders in de gegeven klassen.
Voor de klassen
`0 - 19`
,
`20 - 39`
, is dat anders, omdat je nu het aantal Nederlanders uit twee gegeven klassen bij elkaar op kunt tellen. Met de klassenindeling
`0 - 19`
,
`20 - 39`
...
`60 - 79`
zou je dus wel een nieuw diagram kunnen tekenen.
Je ziet in Voorbeeld 3 een leeftijdsdiagram van de Nederlandse bevolking in 2000.
Welke klassengrenzen heeft de klasse `0-9` ?
Als je het aantal klassen van `9` in `3` verandert, wat is dan de hoogste frequentie?
Waarom is het verhogen van het aantal klassen nu niet mogelijk zonder extra informatie?
Welke van de volgende beweringen zijn juist? Licht je antwoord toe.
In een relatieve frequentietabel of relatieve somfrequentietabel staan altijd percentages.
De totale relatieve somfrequentie is in theorie altijd `100` %.
De totale relatieve somfrequentie is in de praktijk altijd `100` %.
De relatieve frequentie is overal `100` %.
Als er waarnemingen in de laatste klasse vallen, zijn de relatieve somfrequenties lager dan `100` %, behalve bij de laatste klasse.