Voorbeeld 3

Je hebt op 1 januari 2008 een saldo van € 1240,00.
En je besluit dat geld op een spaarrekening te zetten. Verder ga je aan het begin van elke maand
`50`
euro naar die spaarrekening overmaken, te beginnen op 1 februari 2008. Je krijgt aan het eind van elke maand rente van
`0,5`
% over het saldo van dat moment. Je haalt voorlopig geen geld van deze spaarrekening en je doet ook geen andere stortingen.
Wanneer is je saldo meer dan € 3000,00?
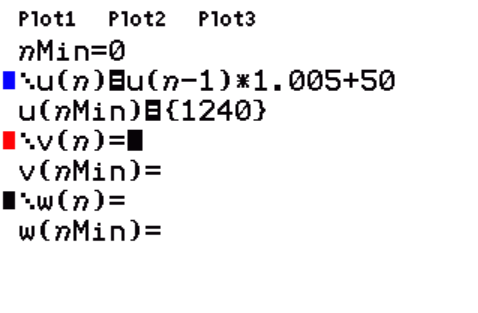
Nu is het maken van een directe formule nog niet eenvoudig. Maar de recursie is wel eenvoudig: je vermenigvuldigt telkens je saldo met `1,005` en telt er `50` euro bij op. Neem je `t=0` op 1-1-2008 en `t` in maanden, dan geldt voor het saldo `S` :
`S(t)=S(t-1 )*1,005 +50` met `S(0 )=1240` .
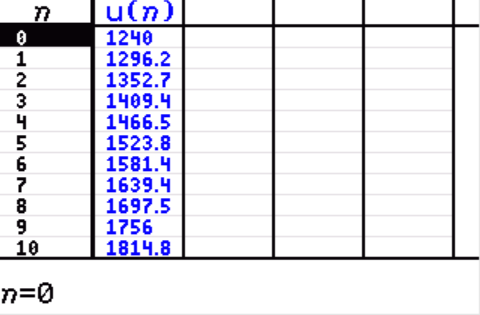
Voer dit in je GR in en bekijk de tabel van de rij. Op `t=30` zit je voor het eerst boven de `3000` euro. Dan heb je `30` maanden gespaard.
|
|
In Voorbeeld 3 wordt bekeken hoe je bij een rij een formule kunt maken. Een directe formule is altijd het handigst, dan hoef je de rij niet vanaf het begin op te bouwen, maar kun je elke waarde direct berekenen. Maar niet altijd is zo'n directe formule gemakkelijk te vinden.
Licht de gevonden recursieformule toe. Waarom moet je bij een recursieformule ook altijd minstens één term van de rij weten?
Laat zien hoe de recursie werkt door met de hand de eerste vier termen van de rij te berekenen. Controleer je antwoorden door op de grafische rekenmachine een tabel te maken bij deze rij.
Hier zie je een aantal rijen waarvan de regelmaat is gegeven. Stel telkens zowel een recursieformule als een directe formule op. Nummer de termen steeds vanaf `0` .
De even getallen: `0` , `2` , `4` , `6` , `8` , ...
De oneven getallen: `1` , `3` , `5` , `7` , `9` , ...
De kwadraten: `1` , `4` , `9` , `16` , `25` , ...
De faculteiten: `1` , `1` , `2` , `6` , `24` , `120` ,...