Voorbeeld 3
De beroemde rij van Fibonacci is:
`1`
,
`1`
,
`2`
,
`3`
,
`5`
,
`8`
,
`13`
,
`21`
,
`34`
, ...
Wat valt je op als je de bijbehorende verschilrij bekijkt?
Bereken de som van de eerste
`100`
termen van de rij van Fibonacci.
De verschilrij is:
`0`
,
`1`
,
`1`
,
`2`
,
`3`
,
`5`
,
`8`
,
`13`
,
`21`
, ...
Behalve de eerste term is de verschilrij gelijk aan de rij zelf, alleen de nummering verschuift met
`2`
. (Denk er om dat er geen nulde term is bij de verschilrij!)
Noem nu de termen van de rij van Fibonacci
`f(n)`
met
`n=0 ,1 ,2 ,...`
Dan is dus de verschilrij:
`∆ f(n)=f(n)-f(n-1 )=f(n-2 )`
.
De rij van Fibonacci heeft daarom als recursieformule:
`f(n)=f(n-1 )+f(n-2 )`
met
`f(0 )=1`
en
`f(1 )=1`
.
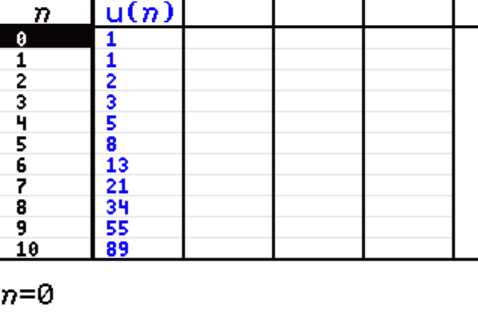
Nu kun je de rij in de grafische rekenmachine invoeren en de som van de eerste `100` termen laten berekenen door de machine. (Het kost wat rekentijd...)

|
|

|
In Voorbeeld 3 maak je kennis met de rij van Fibonacci. Je zult er later nog toepassingen van tegenkomen.
Bekijk hoe de recursieformule van deze rij wordt opgesteld.
Bereken met je grafische rekenmachine de som van de eerste `20` termen van de rij van Fibonacci.
Gegeven is de rij `t(i)=5 i+2` voor `i≥0` .
Stel een formule op voor de verschilrij `V(i)` .
Bereken `sum_(i=0)^(5) t(i)` . Is dit nu de vierde, vijfde of de zesde term van de somrij `S(i)` ? Is het `S(4 )` , `S(5 )` of `S(6 )` ?
Welke termen van `t(i)` moet je optellen om `sum_(i=2)^(5) t(i)` te berekenen? Waarom is dit gelijk aan `S(5 )-S(1 )` ?