Antwoorden van de opgaven
De grafiek die exponentiële groei beschrijft. Bij een recursieformule van deze vorm hoort namelijk een directe formule die er uit ziet als een exponentiële functie, zie de uitleg.
Er is sprake van ongebreidelde groei, dus groter dan `1` .
Als `t` met `1` toeneemt, dan neemt `N` met een factor `1,2` toe en de beginhoeveelheid is `2000` .
`N(t) = 2000 * 1,2^t`
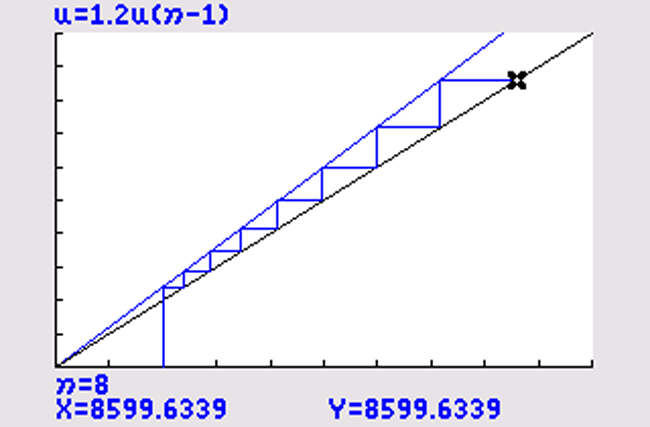
Voer in: `u(n)=1,2u(n-1)` en `u(ntext(Min))={2000}` .
Venster: `[0, 10000]xx[0, 10000]` .
De webgrafiek convergeert niet naar een snijpunt, dus de rij divergeert.
Voer in: `u(n)=u(n-1)+0,2(1-(u(n-1))/4000)*u(n-1)` en `u(ntext(Min))={2000}` .
Venster: `[0, 5000]xx[0, 5000]` .
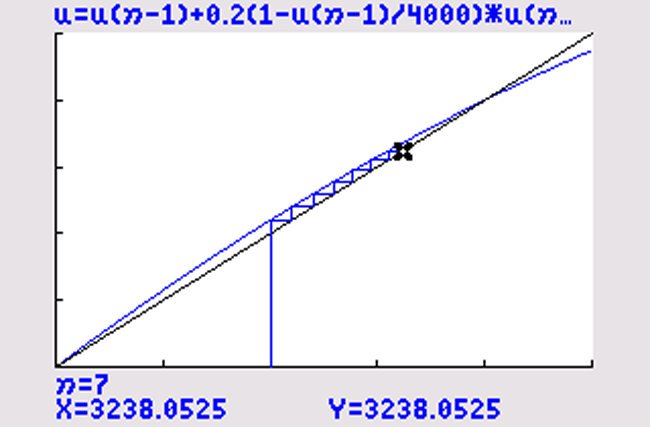
De webgrafiek convergeert naar het snijpunt `(4000, 4000)` .
Als `N(t-1) rarr M` dan `(N(t-1))/M rarr 1` .
Werk de haakjes weg, dan blijkt dat de recursieformule kwadratisch is.
`N(t) = 1,02*N(t-1) - ((N(t-1))^2)/M`
In de evenwichtssituatie is `N(t) = N(t-1) = N` en dan wordt de differentievergelijking:
| `N` | `=` | `N + 0,2 * (1 - N/M) * N` | |
| `0,2 * (1 - N/M) * N` | `=` | `0` | |
| `1 - N/M` | `=` | `0` | |
| `N` | `=` | `M` |
Met behulp van een tijd- of webgrafiek kun je zien dat de rij convergeert.
De grenswaarde volgt uit `N = 0,84N + 200` en dit geeft `N = 200/(0,16) = 1250` .
Met behulp van een tijd- of webgrafiek kun je zien dat de rij divergeert.
Met behulp van een tijd- of webgrafiek kun je zien dat de rij convergeert.
De grenswaarde volgt uit `N = 0,5N(6 - N)` en dit geeft `N = 4` .
`N = aN + b` geeft `(1 - a)N = b` en dit geeft: `N = b/(1 - a)` .
Uitschrijven geeft: `N(t) = d*a^t +b*(a^(t-1) + ... + a + 1)` .
Gebruik de somformule voor de meetkundige rij:
|
`N(t)` |
`=` |
`d*a^t + b*(1 - a^t)/(1 - a)` |
|
|
`` |
`=` |
`d*a^t+b/(1-a)-(b*a^t)/(1-a)` |
|
|
`` |
`=` |
`(d-b/(1-a))*a^t+b/(1-a)` |
Omdat als `0 lt a lt 1` altijd `lim_(t rarr oo) u(t) = b/(1-a)` .
Voer in: `u(n)=u(n-1)+0,05u(n-1)` en `u(ntext(Min))={50}` .
Venster: `[0, 50]xx[0, 500]` .
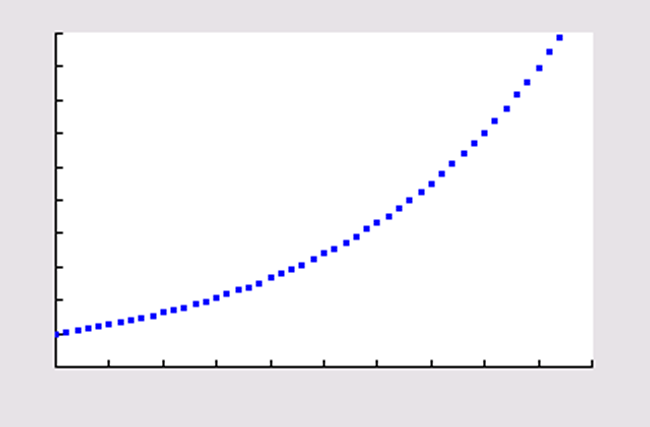
`N(t) = 50 * 1,05^t`
Het aantal bacteriën blijft groeien.
Bijvoorbeeld `N(t) = N(t-1) - 0,4*N(t-1) + 500` met `N(0) = 1600` , waarin `N(t)` het aantal thuja's na `t` jaar voorstelt. Dit is inderdaad een lineaire differentievergelijking van de eerste orde.
De groeivoet is `text(-)0,40` en de groeifactor is `0,60` .
`N(t) = (1600 - 500/(1 - 0,6)) * 0,6^t + 500/(1 - 0,6) = 350 * 0,6^t + 1250`
De grenswaarde is `1250` .
Aan de factor `1,5*(1 - (K(t-1))/600)` .
Als `K(t-1) rarr 600` , dan `1 - (K(t-1))/600 rarr 0` .
|
`y` |
`=` |
`2,5*(1 - x/1000)*x` |
|
|
`` |
`=` |
`2,5x - (x^2)/400` |
|
|
`` |
`=` |
`2,5x-0,0025x^2` |
|
`x` |
`=` |
`2,5x - 0,0025x^2` |
|
|
`0,0025x^2 - 1,5x` |
`=` |
`0` |
|
|
`x(0,0025x-1,5)` |
`=` |
`0` |
|
|
`x` |
`=` |
`0 vv x=600` |
De twee dekpunten zijn `(0, 0)` en `(600, 600)` . Het eerste dekpunt zou worden bereikt als de startpopulatie `0` zou zijn en het tweede dekpunt hoort bij de geschetste situatie.
Nee, tenzij je met `0` of met `1000` of meer snuitkevers begint.
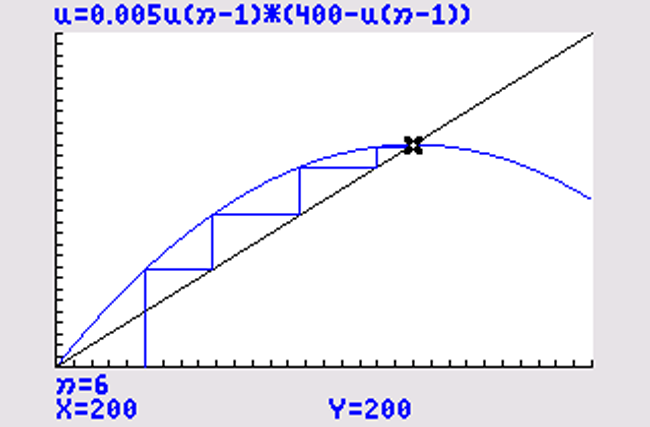
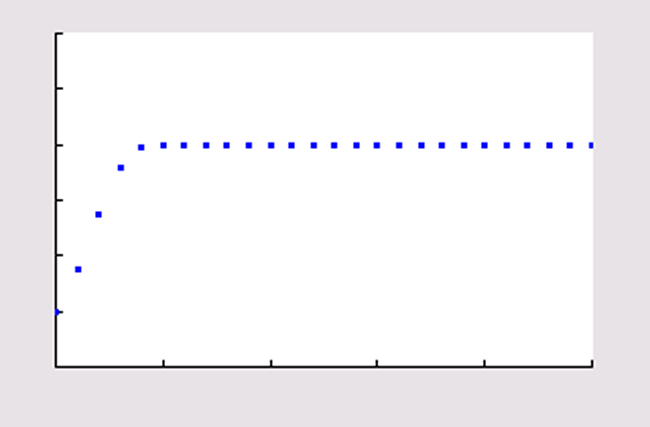
Voer in: `u(n)=0,005u(n-1)*(400-u(n-1))` en `u(ntext(Min))={50}`
Venster voor de webgrafiek: `[0, 300]xx[0, 300]`
Venster voor de tijdgrafiek: `[0, 25]xx[0, 300]`
|
|
Het aantal bacteriën convergeert naar `200` .
|
`N_t` |
`=` |
`0,005*N(t-1)*(400-N(t-1))` |
|
|
`` |
`=` |
`2N(t-1)-0,005(N(t-1))^2` |
|
|
`` |
`=` |
`N(t-1)+N(t-1)-(N(t-1))^2/200` |
|
|
`` |
`=` |
`N(t-1)+(1-(N(t-1))/200)*N(t-1)` |
De groeivoet is `1` .
Uit de factor `(1 - (N(t-1))/200)` . Als `N(t-1) rarr 200` , dan `1 - (N(t-1))/200 rarr 0` .
`y = 0,005x*(400 - x) = 2x - 0,005x^2`
|
`x` |
`=` |
`2x - 0,005x^2` |
|
|
`0,005x^2 - x` |
`=` |
`0` |
|
|
`x(0,005x-1)` |
`=` |
`0` |
|
|
`x` |
`vv` |
`0 vv x=200` |
De twee dekpunten zijn `(0, 0)` en `(200, 200)` . Het eerste dekpunt zou worden bereikt als de startpopulatie 0 zou zijn en het tweede dekpunt hoort bij de geschetste situatie.
Er is dan van groei geen sprake, dit aantal blijft dan steeds hetzelfde.
`x=0,5x+2` geeft `x=4` .
Het dekpunt is `4` .
Omdat `0<0,5<1` is er sprake van convergentie. Dit kun je ook zien in de tijd- of webgrafiek.
`x=1,08x` geeft `x=0` .
Het dekpunt is `0` .
Omdat `1,08>1` is er sprake van divergentie. Dit kun je ook zien in de tijd- of webgrafiek.
`x=5-0,6x` geeft `x=3,125` .
Het dekpunt is `3,125` .
Omdat `text(-)1<text(-)0,6<0` is er sprake van alternerende convergentie. Dit kun je ook zien in de tijd- of webgrafiek.
Bereken het dekpunt door de vergelijking `N = 0,8N + 100` op te lossen. Dit geeft `N = 100/(0,2) = 500` en dit is onafhankelijk van `N(0)` .
Voer in:
`u(n)=0,8u(n -1)+100` en `u(n text(Min))={100}` .
`v(n)=0,8v(n -1)+100` en `u(n text(Min))={500}` .
`w(n)=0,8w(n -1)+100` en `u(n text(Min))={900}` .
Venster: `[0, 50]xx[0, 1000]` .
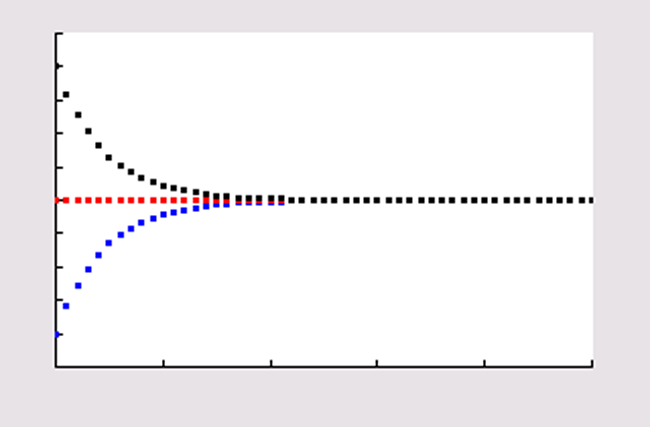
Naar `N = 500` .
`N(0) = 100`
:
`N(t) = text(-)400*0,8^t + 500`
.
`N(0) = 500`
:
`N(t) = 500`
.
`N(0) = 900`
:
`N(t) = 400*0,8^t + 500`
.
Voor alle drie de formules geldt `lim_(n rarr oo) N(t)=500` .
`y=x+0,25x(1-x/100)=1,25x-0,0025x^2`
| `x` | `=` | `x + 0,25 * x * (1 - x/100)` | |
| `0,25*x*(1-x/100)` | `=` | `0` | |
| `x=0` | `vv` | `x=100` |
De dekpunten zijn `0` en `100` .
Voer in: `u(n) = u(n-1) + 0,25 *u(n-1) * (1 - (u(n-1))/100)` en `u(0) = {20}` .
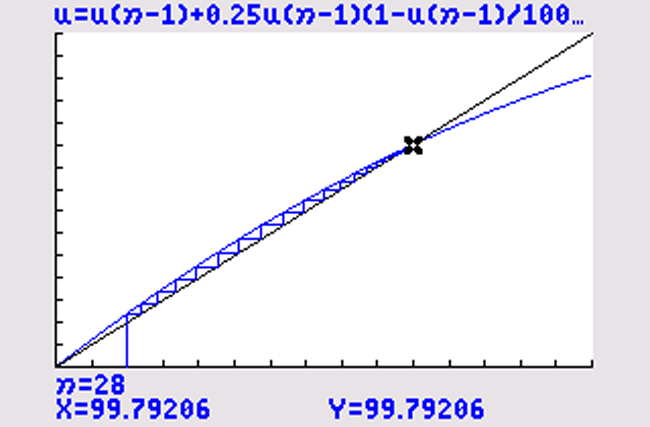
De webgrafiek convergeert naar het snijpunt `(100, 100)` . De rij convergeert.
Als de startwaarde een dekpunt is, dan is de rij constant.
|
`x` |
`=` |
`5x(1-x)+1` |
|
|
`x` |
`=` |
`5x-5x^2+1` |
|
|
`5x^2-4x-1` |
`=` |
`0` |
`x=text(-)0,2 vv x=1` (abc-formule)
Als `N(0)=text(-)0,2 vv N(0)=1` is de rij `N(t)` constant.
| `4800` | `=` | `1,8*4000-a*4000^2` | |
| `a` | `=` | `0,00015` |
| `A_(t)` | `=` | `1,8 * A_(t-1) - 0,00015* (A_(t-1))^2` | |
| `` | `=` | `A_(t-1)+0,8*A_(t-1)-0,00015*(A_(t-1))^2` | |
| `` | `=` | `A_(t-1)+0,8*(1-(A_(t-1))/(5333 1/3))*A_(t-1)` |
Zie de formule in het antwoord van b: `5333` herten.
Er moet gelden dat `K_0=K_1=0,2` .
| `0,2` | `=` | `a*0,2(1-0,2)` | |
| `0,2` | `=` | `0,16a` | |
| `a` | `=` | `1,25` |
Er moet gelden dat `K_2=0,2` en `K_1=0,16a` .
| `K_2` | `=` | `0,16a^2(1-0,16a)=0,2` | |
| `text(-)0,0256a^3+0,16a^2-0,2` | `=` | `0` | |
| `a^3-6,25a^2+7,8125` | `=` | `0` |
Een oplossing voor deze vergelijking is al bekend, namelijk `a=1,25` (zie a).
Ontbind dit in: `(a-1,25)(a^2-5a-6,25)` .
Dus `a=1,25 vv a=(5-sqrt(50))/2 vv a=(5+sqrt(50))/2` .
`a=1,25` voldoet niet, omdat dan de rij constant is.
De andere twee mogelijkheden voldoen wel.
`(25+15)/25 = 1,6`
Voer in: `y=25*1,6^t` of gebruik de recursieformule `u(n)=1,6*u(n-1)` met `u(0)=25` .
Bekijk de tabel.
| week | 0 | 1 | 2 | 3 | 4 | 5 |
| aantal brandnetels | 25 | 40 | 64 | 102 | 164 | 262 |
`N(t) = N(t-1) + 0,6*(1 - (N(t-1))/225)*N(t-1)` met `N(0)=25` .
Hierin is `N(t)` het aantal brandnetels na `t` weken.
Voer in: `u(n)=u(n-1)+0,6*(1-(u(n-1))/225)*u(n-1)` en `u(text(nMin))={25}` .
Bekijk de tabel.
| `t` | 0 | 1 | 2 | 3 | 4 | 5 |
| `N(t)` | 25 | 38 | 57 | 83 | 115 | 148 |
`S(t) = 1,0025S(t-1) - 1500` met `S(0) = 10^6` .
De rij convergeert niet, maar divergeert, het saldo wordt steeds hoger.
`S(t) = 400000 * 1,0025^t + 600000` . Het saldo wordt steeds groter.
Maximaal `2500` euro.
`A(t) = 1,90 * A(t-1)` met `A(0) = 3000` .
`A(t) = 3000 * 1,90^t`
`A = 1,95A - 0,00002A^2` oplossen geeft `A = 0 vv A = 47500` .
`47500` abonnees.