Voorbeeld 2
In de economie wordt als typerend model voor vraag een aanbod de zogenaamde
"varkenscyclus"
gebruikt. Hierbij gaat het erom dat het aanbod
`q_(text(A))(t)`
(van varkens op de varkensmarkt) op een bepaald tijdstip
`t`
afhangt van de prijs
`p(t-1)`
van een periode eerder. De vraag
`q_(text(V))(t)`
wordt echter bepaald door de prijs van dit moment
`p(t)`
.
Verdere modelaannames zijn:
-
Als de prijs toeneemt, neemt de vraag af.
-
Als de prijs toeneemt, neemt het aanbod toe.
-
Zowel vragers als aanbieders reageren onmiddellijk op elke prijsverandering.
-
Alles wat wordt aangeboden wordt meteen verkocht.
Hierbij passen modelformules zoals:
`q_(text(A))(t) = p(t-1) - 25`
en
`q_(text(V))(t) = 400 - 1,5p(t)`
.
Reken dit model door met een startprijs
`p(0) = 120`
en zoek de prijs waarbij vraag en aanbod elkaar in evenwicht houden.
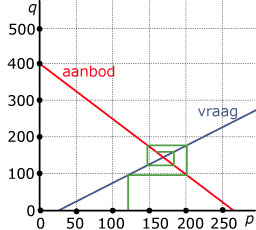
Breng dit model in beeld door de lijnen `q_(text(A)) = p - 25` en `q_(text(V)) = 400 - 1,5p` in één assenstelsel te tekenen. Start bij `p(0) = 120` , bepaal eerst `q_(text(A))` en bepaal dan bij welke prijs `q_(text(V))` even groot is. Bepaal bij die `p(1)` weer `q_(text(A))` en herhaal het voorgaande.
Om dit model op de grafische rekenmachine in te voeren, stel je voor
`p(t)`
een differentievergelijking op uitgaande van
`q_(text(A)) = q_(text(V))`
.
Deze wordt:
`p(t-1) - 25 = 400 - 1,5p(t)`
.
Dit geeft
`p(t) = 283 1/3 - 2/3 * p(t-1)`
en hieruit blijkt hoe de rij
`p(t)`
convergeert naar een evenwichtsprijs.
In Voorbeeld 2 tref je een economisch model aan dat de varkenscyclus wordt genoemd. Er zijn twee modelvergelijkingen gegeven.
Leg uit dat beide modelvergelijkingen voldoen aan de eerste twee aannames.
Laat met een tijdgrafiek zien dat de rij `p(t)` convergeert.
Stel een directe formule op voor `p(t)` en bereken daarmee de grenswaarde die `p(t)` nadert.
Bekijk de grafiek in het voorbeeld waarin de prijsontwikkeling is aangegeven.
Waarom is dit niet de webgrafiek van de rij `p(t)` ?
Hoe kun je uit de oorspronkelijke modelformules de grenswaarde van `p(t)` berekenen?
Een dynamisch vraag- en aanbodmodel wordt gegeven door `q_(text(A))(t) = 2 + p(t-1)` en `q_(text(V))(t) = 16 - 4/3 p(t)` met `t` in maanden. `q_(text(A))` stelt de aangeboden hoeveelheid van een bepaald artikel voor en `q_(text(V))` is de op de handelsmarkt gevraagde hoeveelheid van ditzelfde artikel. Neem `p_0 = 3` .
Waarom komt in de formule voor de vraag `p(t)` voor en in die voor het aanbod `p(t-1)` ?
Stel een recursieformule op voor `p(t)` uitgaande van `q_A=q_V` en laat met een tijdgrafiek zien dat de rij `p(t)` convergeert.
Stel een directe formule op voor `p(t)` en bereken daarmee de grenswaarde die `p(t)` nadert.
Teken een grafiek waarin je de prijsontwikkeling aangeeft met behulp van de grafieken van `q_(text(A)) = 2 + p` en `q_(text(V)) = 16 - 4/3 p` .