Voorbeeld 3

In veel natuurgebieden is er sprake van een wisselwerking tussen de roofdieren en hun prooi, zoals vossen en konijnen. Modellen die zo'n wisselwerking bestuderen heten "roofdier-prooi-modellen" . De Italiaanse wiskundige Vito Volterra en de Amerikaanse wiskundige Alfred J. Lotka ontwierpen in 1925-1926 een dynamisch model voor dergelijke wisselwerkingen. Als `P(t)` het aantal prooidieren en `R(t)` het aantal roofdieren op tijdstip `t` is, zien de vergelijkingen er in discrete vorm als volgt uit:
-
`P(t) = P(t-1) + (a - b * R(t-1))*P(t-1)`
-
`R(t) = R(t-1) - (c - d * P(t-1))*R(t-1)`
Hierin zijn
`a`
,
`b`
,
`c`
en
`d`
positieve getallen.
Neem
`a = 0,20`
,
`b = 0,0015`
,
`c = 0,1`
en
`d = 0,0002`
. Ga verder uit van
`P(0) = 600`
dieren en
`R(0) = 100`
dieren. De tijd
`t`
is in maanden.
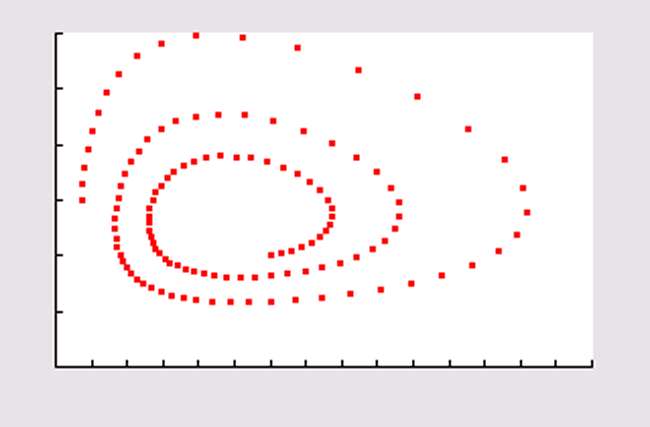
Plot met de grafische rekenmachine een grafiek waarin je het aantal prooidieren uitzet tegen het aantal roofdieren voor deze `120` maanden. Hoe zie je aan deze grafiek dat dit model periodiek is met een zekere stijgingstrend?
Voer in:
`u(n)=u(n-1)+(0,2-0,0015*v(n-1))*u(n-1)` en `u(ntext(Min))={600}` .
`v(n)=v(n-1)-(0,1-0,0002*u(n-1))*v(n-1)` en `u(ntext(Min))={100}` .
Venster: `[0, 150]xx[0, 300]` .
Kies voor de fasegrafiek, zie het Practicum.
De grafiek ziet eruit als een langzaam naar buiten spiralende kromme.
Bekijk het roofdier-prooi-model in Voorbeeld 3.
Waarom komt in de formule voor het aantal roofdieren een minteken voor `(c - d * P(t-1))*R(t-1)` ?
Voer de recursieformules in op de grafische rekenmachine en plot een tijdgrafiek voor de eerste `120` maanden.
Na hoeveel maanden heeft het aantal prooidieren voor het eerst een maximale waarde bereikt? Waardoor wordt de daling van het aantal prooidieren daarna veroorzaakt?
Ga na dat het model periodiek is met een zekere stijgingstrend.
In een afgesloten gebied leven konijnen en vossen. Voor de groeifactor van het aantal konijnen geldt `g_(text(k)) = 1,15 - 0,01 * V(t)` en voor de groeifactor van het aantal vossen geldt `g_(text(v)) = 0,70 + 0,0002 * K(t)` . Hierin is `K(t)` het aantal konijnen in jaar `t` en `V(t)` het aantal vossen in jaar `t` . Neem aan dat `V(0) = 20` en `K(0) = 2500` dieren.
Licht toe dat hierbij het roofdier-prooi-model past dat in Voorbeeld 3 is beschreven.
Welke twee modelformules kun je op grond hiervan opstellen voor het verloop van de aantallen dieren van deze twee soorten?
Voer de recursieformules in op de grafische rekenmachine en plot een tijdgrafiek voor de eerste `70` maanden.
Na hoeveel jaar heeft het aantal vossen voor het eerst een maximale waarde bereikt? Wat betekent dit voor het aantal konijnen daarna?
Is dit model voor beide diersoorten op den duur gunstig?