Uitleg
Figuur opent via muisklik
Dan draaibaar met rechter muisknop
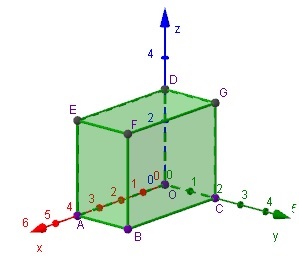
In de ruimte kun je elk punt van coördinaten voorzien door een `x` -as, een `y` -as en een `z` -as loodrecht op elkaar te zetten en van dezelfde schaalverdeling te voorzien. Het snijpunt van de drie assen is `O` . Je hebt dan een driedimensionaal cartesisch assenstelsel, ook wel aangeduid met `RR^3` .
Hier zie je een driedimensionaal cartesisch
`Oxyz`
-assenstelsel met balk
`OABC.DEFG`
.
Punt
`F`
heeft de coördinaten
`(4, 2, 3)`
.
Je ziet eerst de
`x`
-coördinaat, dan de
`y`
-coördinaat en tenslotte de
`z`
-coördinaat.
De coördinaten van enkele andere hoekpunten zijn:
`O(0, 0, 0)`
,
`A(4, 0, 0)`
,
`B(4, 2, 0)`
en
`D(0, 0, 3)`
.
In een 3D assenstelsel kun je ook werken met vectoren, alleen in plaats van twee componenten heb je nu drie componenten. Zo geldt voor de vector die van
`O`
naar
`F`
gaat:
`vec(OF) = ((4),(2),(3))`
Verder heb je bijvoorbeeld de vectoren:
`vec(OE) = ((4),(0),(3))`
,
`vec(EG) = ((text(-)4),(2),(0))`
en
`vec(AG) = ((text(-)4),(2),(3))`
Ook het midden van een lijnstuk kun je op dezelfde manier berekenen als in een gewoon tweedimensionaal assenstelsel. Ga na dat voor het midden `M` van lijnstuk `BF` geldt: `M((4+4)/2, (2+2)/2, (0+3)/2) = M(4; 2; 1,5)`
De lengte van `vec(OF)` kan worden berekend door de stelling van Pythagoras uit te breiden naar drie dimensies: `|vec(OF)| = sqrt(4^2 + 2^2 + 3^2) = sqrt(29)` .
Bekijk Uitleg 1. Werken met coördinaten en vectoren in drie dimensies is in veel gevallen een eenvoudige uitbreiding van het werken in twee dimensies.
Beschrijf de vectoren `vec(CE)` , `vec(EC)` , `vec(DF)` en `vec(DB)` met kentallen.
Bereken het midden `N` van lijnstuk `EG` . Laat zien dat `N` ook het midden van lijnstuk `DF` is.
Laat zien door twee keer de stelling van Pythagoras in een rechthoekige driehoek toe te passen hoe de lengte van `vec(OF)` wordt berekend.
Bereken de lengtes van de vectoren `vec(CE), vec(EC)` en `vec(DF)` .
Bekijk in Uitleg 1 hoe je afstanden tussen twee punten kunt berekenen in 3D.
Bereken de afstand tussen de punten `B` en `D` .
`M` is het midden van `BF` en `N` is het midden van `EG` .
Bereken `|vec(MN)|` .
Waar liggen in een 3D cartesisch assenstelsel alle punten `(x, y, z)` waarvoor geldt:
De `x` -coördinaat is `4` (dus `x=4` ).
De `z` -coördinaat is `0` (dus `z=0` ).
De `y` -coördinaat is hetzelfde als de `z` -coördinaat (dus `y=z` ).