Uitleg
Figuur opent via muisklik
Dan draaibaar met rechter muisknop
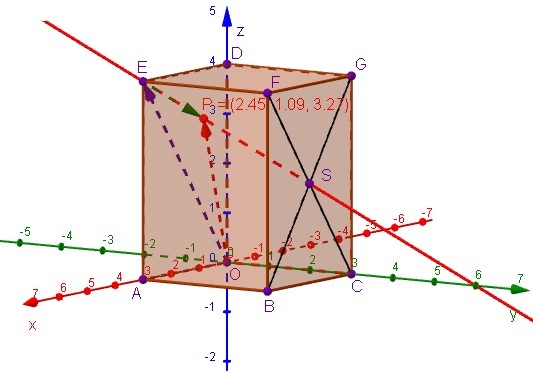
Je ziet hier een balk `OABC.DEFG` met punt `S` als snijpunt van `BG` en `CF` . Er is een lijn getrokken door de punten `E` en `S` . Punt `P` is een punt dat over deze lijn beweegt.
Bij elk punt
`P`
hoort een plaatsvector (of steunvector)
`vec(OP) = vec(OE) + t*vec(ES)`
Dus met kentallen:
`((x),(y),(z)) = ((3),(0),(4)) + t*((text(-){:1,5:}),(3),(text(-)2))`
.
Dit noem je een vectorvoorstelling van de lijn waar
`P`
op ligt.
`vec(ES) = vec(r)`
is een richtingsvector en
`vec(OE) = vec(p)`
is een plaatsvector van de lijn.
Je kunt bijvoorbeeld ook `vec(OS)` als plaatsvector en `vec(SE)` als richtingsvector kunnen kiezen. En zo zijn er meer mogelijkheden: de plaatsvector is een vector vanuit `O` naar een punt op de lijn, de richtingsvector is een vector tussen twee punten op de lijn.
Elk punt `P` op de lijn heeft coördinaten `(x, y, z)=(3 - 1,5t; 3t; 4 - 2t)` , hierin is `t` de parameter. Het is niet mogelijk om in 3D een lijn te beschrijven door middel middel van een vergelijking, alleen door een vectorvoorstelling of een parametervoorstelling.
Als je binnen één context/opgave een tweede lijn, bijvoorbeeld lijn `BG` wilt beschrijven, moet je een andere letter voor de parameter gebruiken (vaak worden ook wel de griekse letters `lambda` en `mu` gebruikt).
De hoek tussen twee lijnen is de hoek tussen hun richtingsvectoren (wel altijd de scherpe hoek). Die bereken je met het inproduct.
Bekijk Uitleg 1. Bekijk wat een vectorvoorstelling van een lijn is.
Waarom is `((x),(y),(z))=(({:1,5:}),(3),(2))+p*(({:1,5:}),(text(-)3),(2))` ook een vectorvoorstelling van de getekende lijn? Welke vectoren zijn dan de plaatsvector en de richtingsvector?
En is `((x),(y),(z))=(({:1,5:}),(3),(2))+p*((3),(text(-)6),(4))` ook een geschikte vectorvoorstelling? Licht je antwoord toe.
Waarom kun je een lijn in 3D niet beschrijven met een vergelijking?
Hoe zien de vectorvoorstellingen van de assen er uit?
Bekijk de figuur in Uitleg 1.
Stel een vectorvoorstelling op van de lijn `BG` .
Bereken de hoek die de lijnen `SE` en `BG` met elkaar maken.
Je ziet in de figuur dat de lijnen `ES` en `BG` elkaar in `S` snijden.
Laat zien, dat punt `S` zowel aan de vectorvoorstelling van `ES` als aan die van `BG` voldoet.
Je kunt de coördinaten van `S` ook krijgen door de `x` -waarden, de `y` -waarden en de `z` -waarden van beide lijnen gelijk te stellen. Je krijgt dan drie vergelijkingen met daarin twee onbekende parameters.
Bereken die parameters vanuit twee van de gevonden vergelijkingen. Controleer dat de gevonden waarden ook aan de derde vergelijking voldoen en dat je de coördinaten van `S` krijgt.