Krommen en oppervlakken

Krommen en oppervlakken > Kegels en kegelsneden

123456Kegels en kegelsneden

Uitleg

Figuur opent via muisklik
Dan draaibaar met rechter muisknop

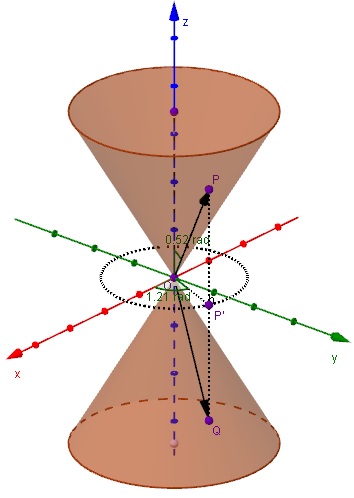
Een kegeloppervlak bestaat uit alle punten `P` die een recht evenredig toenemende afstand hebben tot een vaste lijn `a` . `a` heet de as van de kegel en het punt waar de afstand tot de as `0` is heet de top `T` . De afstand van `P` tot de as wordt bepaald door de halve tophoek `varphi` , dat is de hoek tussen de as en de lijn `TP` .

Is `O(0, 0, 0)` de top en de `z` -as de as van de kegel, dan ligt elk punt `P(x, y, z)` op een cirkel met straal `r=z * tan(varphi)` . En omdat `|OP'|^2=x^2+y^2=r^2` vind je
`x^2+y^2=z^2 * tan^2(varphi)`
Dit is de vergelijking van een kegel(oppervlak) met de `z` -as als as, `O` als top en `varphi` als halve tophoek.

Je kunt deze vergelijking eenvoudig aanpassen voor het geval de top `T(a, b, c)` en de as evenwijdig met één van de coördinaatassen is. Ook een parametervoorstelling is mogelijk.

Opgave 1

Bekijk Uitleg 1. Je ziet een kegel $K$ met top $O (0, 0, 0)$ , de $z$ -as als symmetrieas en een halve tophoek $φ = \frac{1}{6} π$ .

Neem nu aan dat punt $P$ op de kegel $K$ een $z$ -waarde van $5$ heeft. Bereken dan de straal van de cirkel waar $P$ op ligt.

Bereken nu de $y$ -coördinaat van $P$ als de $x$ -coördinaat $3$ is.

Voor een ander punt $P$ geldt $x = - 3$ en $y = 2$ . Bereken de $z$ -waarden die dit punt $P$ kan hebben.

Aan welke vergelijking moeten de punten $P (x, y, z)$ voldoen als $P$ op de kegel ligt?

Leid nu zelf de algemene vergelijking af van een kegel met top $O (0, 0, 0)$ , de $z$ -as als symmetrieas en een halve tophoek $φ$ .

Opgave 2

Natuurlijk hoeft een kegel niet de $z$ -as als as te hebben en de oorsprong als top.

Stel een vergelijking op van een kegel met de $x$ -as als symmetrieas, de oorsprong als top en een halve tophoek van $\frac{1}{4} π$ .

Laat zien, dat een "kegel" met een halve tophoek van `0^@` een rechte lijn oplevert. Neem bijvoorbeeld de $x$ -as als symmetrieas en de oorsprong als top.

Welke waarden kan de halve tophoek aannemen?

Stel een vergelijking op van een kegel met top $T (1, 2, 3)$ , een as evenwijdig aan de $y$ -as die door het punt $(2, 0, 0)$ gaat.

verder | terug