Antwoorden van de opgaven
Zie de Uitleg 1.
-
`0 le x le 50` (maximaal `50` fietsen)
-
`y ge 0` (geen beperkingen voor e-bikes)
-
`500x + 900y le 95000` (er is maximaal € 95000,00 om fietsen en e-bikes in te kopen)
-
`0,5x + 0,5y le 60` (er is maximaal `60` m2 opslag)
Zie voor de figuur de uitleg. Gebruik je GR met venster `[0, 50]xx[0, 120]` .
Bij `W = 30000` hoort `y_3 = (300-2x)//3` .
Bij `W = 20000` hoort `y_3 = (200-2x)//3` .
Je moet het snijpunt van de grenslijnen `500x+900y = 95000` en `0,5x+0,5y=60` bepalen. Uit de tweede vergelijking volgt `x = 120-y` . Vul dit in de eerste vergelijking in:
| `500(120-y)+900y` | `=` | `950000` | |
| `400y` | `=` | `35000` | |
| `y` | `=` | `87,5` |
De bijbehorende
`x`
-waarde is
`x = 32,5`
.
De maximale winst vind je in het punt
`(32,5; 87,5)`
.
Maar omdat je geen halve fietsen en e-bikes kunt verkopen kijk je naar de vier punten met gehele `x` en `y` om dit punt heen. Alleen de twee punten `(32, 87)` en `(33, 87)` liggen binnen het toegestane gebied. Bereken voor de beide punten de winst. Het punt `(33, 87)` levert de meeste winst op, namelijk `W = 200*33+300*87 = 32700,00` euro.
In `O(0, 0)` .
`x` is het aantal fietsen en `y` het aantal e-bikes per week.
-
`0 le x le 120`
-
`0 le y le 70`
-
`x + y le 140`
-
`x + 2y le 180`
Gebruik je GR met venster `[0, 120]xx[0, 100]` .
Neem `y_1 le 140-x` , `y_2 le 90-0,5x` en `y_3 le 70` .
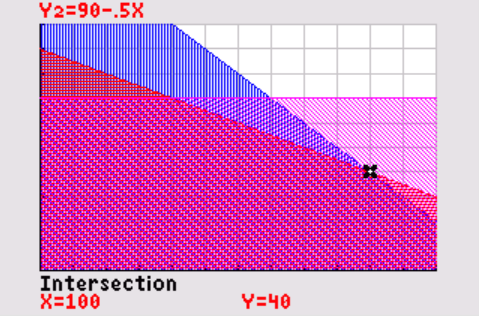
De winst op een fiets bedraagt € 150,00 en op een e-bike € 450,00. Dit geeft `W = 150x+450y` als doelfunctie. De niveaulijnen zijn:
-
`20000 = 150x + 450y` en dit geeft: `y = 44 4/9 - 1/3 x`
-
`30000 = 150 x + 450y` en dit geeft: `y = 66 2/3 - 1/3 x`
De winst is maximaal in het snijpunt van de lijnen `x+2y = 180` en `y = 70` . Dan is `x = 40` . Het snijpunt is `(40, 70)` .
`W = 150*40+450*70 = 37500,00` euro.
De doelfunctie is `W = 0,5x+0,8y` en de randvoorwaarden zijn:
-
`0 le x le 80`
-
`y ge 0`
-
`1,20x+1,50y le 120`
-
`x+2y le 124`
Gebruik je GR met venster `[0, 80]xx[0, 100]` .
Neem `y_1 le 80 - 0,8x` en `y_2 le 62 - 0,5x` .
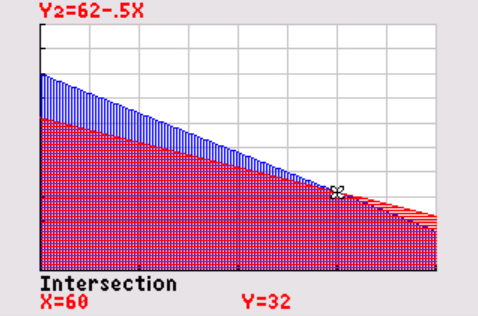
De hoekpunten van het toegestane gebied zijn:
`O(0, 0)`
,
`A(80, 0)`
,
`B(80, 16)`
,
`C(60, 32)`
en
`D(0, 62)`
.
De winst `W` in deze punten is achtereenvolgens:
-
in `O` : `W = 0` euro;
-
in `A` : `W = 0,5*80+0,8*0 = 40,00` euro;
-
in `B` : `W = 0,5*80+0,8*16 = 52,80` euro;
-
in `C` : `W = 0,5*60+0,8*32 = 55,60` euro;
-
in `D` : `W = 0,5*0+0,8*62 = 49,60` euro.
De maximale winst `W` wordt in punt `C` behaald.
Als de grafiek van de winstfunctie (doelfunctie) evenwijdig loopt met één van de lijnstukken (grenzen) van het toegestane gebied
Nu is de doelfunctie `W = 0,80x+0,40y` , deze functie loopt evenwijdig met de lijn `0,4x+0,2y = 6000` . Dat betekent dat de maximale winst in alle punten op het lijnstuk `MN` wordt behaald. Vul de coördinaten van punt `M` in. Deze maximale winst is nu `W = 0,80*6000+0,40*18000 = 12000,00` euro.
`x` en `y` hebben nu niet langer maximale waarden. Dit heeft geen invloed op de maximale winst.
De doelfunctie wordt `W = 0,70x + 0,50y` en de randvoorwaarden zijn:
-
`0 le x le 12000`
-
`0 le y le 20000`
-
`0,3x + 0,2y le 6000`
-
`0,2x + 0,3y le 6000`
Gebruik de GR met venster `[0, 12000]xx[0, 30000]` .
Voer in: `y_1 le 30000 - 1,5x` , `y_2 le 20000 - 2/3 x` en `y_3 le 20000` .
De niveaulijnen worden `y_4 = 10000-1,4x` en `y_5 = 20000-1,4x` .
`W`
is maximaal op het toegestane gebied in
`(12000, 12000)`
.
Van beide melanges zijn dat
`12000`
pakken.
`W = 0,70 * 12000 + 0,50 * 12000 = 144000,00`
euro.
Gebruik de GR met venster `[5, 32]xx[0, 30000]` .
Voer in: `y_1 le 43 - 0,6x` en `y_2 le 26 - 1,2 x` .
Teken de niveaulijnen bij `W=10` en `W=20` .
De niveaulijnen worden `y_3 = 10-2x` en `y_4 = 20-2x` .
Bereken eerst de coördinaten van alle hoekpunten die het toegestane gebied vormen.
`W`
is minimaal in
`(0, 20)`
, namelijk
`W=20`
.
`W`
is maximaal in
`(32, 24)`
, namelijk
`W=87`
.
Omdat `x` en `y` beide groter dan `0` moeten zijn (zie de eerste twee voorwaarden), geldt automatisch dat: `20+x+y ge 0` .
`K`
is minimaal in het punt
`(50, 0)`
.
`K`
is dan
`960`
.
| New York | Londen | |
| Koeweit | `140000` | `60000` |
| Galveston | `100000` | `50000` |
| Caracas | `60000` | `40000` |
De transportkosten zijn in dat geval:
`K = 0,38*140000+0,35*60000+0,10*100000+0,22*50000+`
`0,18*60000+0,25*40000 = 116000`
dollar.
Het minimum is `104500` dollar.
(naar: examen vwo wiskunde A in 1983, eerste tijdvak)
Gebruik de GR met venster `[0, 50]xx[0, 80]` .
Voer in: `y_1 le 80 - 0,5x` , `y_2 le 400 - 4x` en `y_3 le 60` .
Teken de niveaulijnen bij `W = 10` en `W = 20` .
De niveaulijnen worden `y_3 = 10-2x` en `y_4 = 20-2x` .
Teken enkele niveaulijnen. Het maximum zit bij het snijpunt van de lijnen `x + 2y = 160` en `4x + y = 400` . Dat snijpunt is `M(640/7, 240/7)` .
Het maximum is
`W(640/7, 240/7) = 880/7 =125 5/7`
.
Het minimum is
`W(0, 0) = 0`
.
De beslissingsvariabelen zijn het aantal kinderfietsen
`x`
en het aantal e-bikes
`y`
.
De randvoorwaarden, uitgedrukt als ongelijkheden zijn:
-
`0 le x le 40` en `y ge 0`
-
`250x + 1000y le 48000`
-
`0,5x + y le 50`
De doelfunctie is de winstfunctie: `W = 200x + 450y` .
`W = 9000` geeft niveaulijn `y = 20 - 4/9x` en `W = 18000` geeft niveaulijn `y = 40 - 4/9x` .
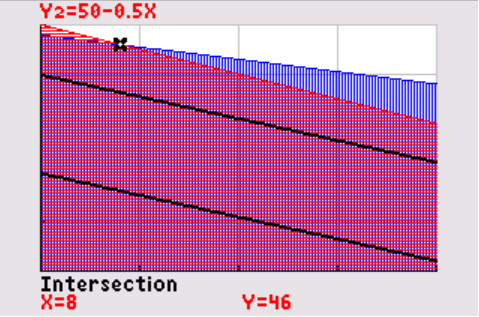
De maximale winst wordt bereikt in het snijpunt van de lijnen `250x + 1000y = 48000` en `0,5x + y = 50` . Uit de tweede vergelijking volgt `y=50-0,5x` . Dit invullen in de eerste vergelijking geeft:
| `250x+1000(50-0,5x)` | `=` | `48000` | |
| `text(-)250x` | `=` | `text(-)2000` | |
| `x` | `=` | `8` |
Het snijpunt is
`(8, 46)`
.
De maximale winst is
`W(8, 46) = 200*8+450*46 = 22300,00`
euro.
Het snijpunt `(8, 46)` verandert daardoor niet en daarom blijft de winst maximaal.
Laat
`a`
het aantal kg aardappelen en
`b`
het aantal kg bonen zijn dat per pak nodig is.
De randvoorwaarden zijn dan:
-
eiwit: `25a+50b ge 13`
-
zetmeel: `400a+200b ge 100`
-
vet: `40a+40b ge 18`
-
`a ge 0` en `b ge 0`
De kostenfunctie per pak is:
`K = 0,15*a+0,20*b`
Teken het toegestane gebied met twee niveaulijnen.
De kosten zijn minimaal in het snijpunt `B` van de lijnen `25a+50b = 13` en `40a+40b = 18` .
De bijbehorende waarde voor `a` is `a = 0,38` .
De minimale kosten per pak liggen bij `0,38` kg aardappelen en `0,7` kg bonen per pak. De kosten bedragen dan `K = 0,15*0,38+0,20*0,07 = 0,071` euro per pak, dat is € 7,10 per `100` pakken.
`1`
kg aardappelen levert
`25+400+40 = 465`
gram aan voedingsstoffen en
`1`
kg bonen
`50+200+40 = 290`
gram.
Het gaat nu om de doelfunctie
`G = 0,465a+0,29b`
, deze moet minimaal zijn.
Het gewicht is minimaal in het snijpunt `C` van de lijnen `40a+40b = 18` en `400a+200b = 100` .
De bijbehorende waarde van `b` is `b = 0,40` .
Per pak is het gewicht minimaal
`G = 0,465*0,05+0,29*0,40 = 0,13925`
kg.
Per
`100`
pakken is dat
`13,925`
kg ofwel
`13925`
gram (bij
`5`
kg aardappelen en
`40`
kg bonen).
Als er `x` eenheden van Nederland naar A en `y` eenheden van Nederland naar B worden getransporteerd, dan ligt de rest vast:
| naar A | naar B | naar C | |
| fabriek NL | `x` | `y` | `5000-x-y` |
| fabriek CN | `3000-x` | `4500-y` | `7000-(3000-x)-(4500-y)` |
| totaal | `3000` | `4500` | `4500` |
De randvoorwaarden:
-
`0 le x le 3000`
-
`0 le y le 4500`
-
`x + y le 5000`
-
`x + y ge 500`
De transportkosten zijn:
`K = 4x+2y+5(5000-x-y)+5(3000-x)+2(4500-y)+3(x+y-500) = `
`47500-3x-2y`
.
Gebruik de GR met venster `[0, 50]xx[0, 5000]` .
Voer in: `y_1 le 5000 - x` , `y_2 le 500 - x` en `y_3 le 4500` .
Uit de figuur met het toegestane gebied en twee niveaulijnen blijkt dat de minimale kosten worden bereikt in punt `(3000, 2000)` . Dan gaan er `3000` eenheden vanuit Nederland naar A, `2000` naar B en `0` naar C. De kosten zijn dan `K = 47500-3*3000-2*2000 = 34500,00` euro.
Het aantal aluminium rackets `x` en het aantal kunststof rackets `y` .
Randvoorwaarden:
-
`x ge 0` en `y ge 0`
-
`25` machines: `25/30x+25/150y le 25` ofwel `5x + y le 150`
-
`20` mensen: `1/2x+1/5y le 20` ofwel `5x + 2y le 200`
De fabriek wil maximale winst behalen. De winstfunctie is: `W = 55x + 20y` .
Gebruik de GR met venster `[0, 50]xx[0, 80]` .
Voer in: `y_1 le 150 - 5x` en `y_2 le 100 - 2,5x` .
Teken de niveaulijnen bij `W = 500` en `W = 1500` .
De niveaulijnen worden `y_3 = 25-2,75x` en `y_4 = 75-2,75x` .
De maximale winst wordt bereikt in het snijpunt `M` van de lijnen `5x+y = 150` en `5x+2y = 200` . Herleid de eerste vergelijking tot `y = 150-5x` . Dit invullen in de tweede vergelijking geeft:
| `5x+2(150-5x)` | `=` | `200` | |
| `text(-)5x` | `=` | `text(-)100` | |
| `X` | `=` | `20` |
De bijbehorende
`y`
-waarde is
`y = 50`
.
Het snijpunt is
`M(20, 50)`
.
De maximale winst is
`W(20, 50) = 55*20+20*50 = 2100,00`
euro per dag.
Voorwaarde
`5x+yle150`
verandert in
`5x+y le 156`
, want het aantal machines neemt met
`4`
% (
`1/25`
deel) toe. Dat betekent ook dat het aantal rackets met
`4`
% toeneemt, van
`150`
naar
`156`
.
Het snijpunt
`M`
van lijn
`5x+y = 156`
met lijn
`5x+2y = 200`
. Uit de eerste vergelijking volgt
`y = 156-5x`
, dit invullen in de tweede vergelijking geeft:
| `5x+2(156-5x)` | `=` | `200` | |
| `text(-)5x` | `=` | `text(-)112` | |
| `x` | `=` | `22,4` |
De bijbehorende
`y `
-waarde is
`44`
.
Je kunt niet
`22,4`
aluminium rackets maken, zodat
`x = 22`
, maar dan kan
`y`
wel nog net
`45`
zijn.
De maximale winst is
`W(22, 45)=55*22+20*45=2110,00`
euro per dag.
Voorwaarde
`5x+2y le 200`
verandert in
`5x+2y le 210`
, want het aantal werknemers neemt met
`5`
% (
`1/20`
deel) toe. Dat betekent dat het aantal rackets met
`5`
% toeneemt, van
`200`
naar
`210`
.
Het snijpunt
`M`
van lijn
`5x+y = 150`
met lijn
`5x+2y = 210`
is nu
`M(18, 60)`
.
De maximale winst is `W(18, 60) = 55*18+20*60 = 2190,00` euro per dag.
De verhoudingen sinaasappel en perzik:
| Sizik `= x` | Pernaas `= y` | |
| sinaasappelsap | 18 | 15 |
| perziksap | 4 | 1 |
| 22 | 16 |
Voor sinaasappelsap geldt de randvoorwaarde:
`4/22 x + 1/16 y le 1000`
ofwel
`2/11 x + 1/16y le 1000`
met grenslijn
`y = 16000 - 2 10/11 x`
.
Voor perziksap geldt randvoorwaarde:
`18/22 x + 15/16 y le 6600`
ofwel
`9/11 x + 15/16 y le 6600`
met grenslijn
`y = 7040 - 48/55 x`
.
Verdere randvoorwaarden zijn:
`x ge 0`
en
`y ge 0`
.
De doelfunctie is de winstfunctie
`W = 1000/2200 x + 500/1600 y`
ofwel
`W = 5/11 x + 5/16 y`
.
Met niveaulijnen of de randenwandelmethode is zichtbaar dat het snijpunt tussen de twee eerder genoemde grenslijnen de maximale winst oplevert. Dan geldt:
`16000 - 2 10/11 x = 7040 - 48/55 x`
Hieruit volgt:
`x = 4400`
L Sizik en
`y = 3200`
L Pernaas en dat levert een maximale winst
`W = 5/11 * 4400 + 5/16 * 3200 = 3000,00`
euro op.
`4400`
liter Sizik bestaat voor
`18/22`
deel uit sinaasappel ofwel uit
`3600`
liter sinaasappelsap.
`3200`
liter Pernaas bestaat uit
`15/16`
deel uit sinaasappelsap ofwel uit
`3000`
liter sinaasappelsap.
Samen is dat
`6600`
liter sinaasappelsap en dat is precies wat de fabrikant had ingekocht.
Zo blijkt ook dat er respectievelijk
`800`
en
`200`
liter perziksap is gebruikt en dat is samen precies de ingekochte
`1000`
liter perziksap.
-
`x ge 0` en `y ge 0`
-
`x+3y le 75`
-
`x ge 3y` en `x le 8y`
-
`y le 10`
Zie figuur. GR met venster `[0, 60]xx[0, 30]` .
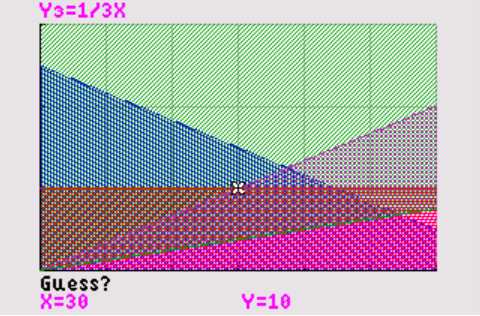
De opbrengstfunctie is: `O = 8x+20y` .
Het maximum wordt bereikt in het snijpunt
`M`
van de lijnen
`x = 8y`
en
`x+3y = 75`
. Substitueren van de eerste vergelijking in de tweede geeft
`11y = 75`
, ofwel
`y = 75/11`
en dan is
`x = 600/11`
. Maar omdat het om aantallen gaat, moeten
`x`
en
`y`
geheel zijn. Het roosterpunt dat het dichtst in de buurt van
`M`
ligt (en binnen het toegestane gebied) is
`(54, 7)`
.
De opbrengst is maximaal bij
`54`
auto's en
`7`
autobussen:
`O = 8*54+20*7 = 572,00`
euro.
Grenslijn voorwaarde B:
Er is ten minste
`2,8x`
m3 boven
`1,80`
m nodig.
Er is 200 m2 vloeroppervlak, zodat er ten minste
`(2,8x)/200 = 0,014x`
m hoogte boven
`1,80`
m nodig is. Daar komt dan nog
`1,80`
m bij, zodat
`h ge 0,014x + 1,8`
met een vergelijkbare grenslijn.
Voorwaarde B is het strengst op het gedeelte tussen de twee snijpunten.
Grenslijn voorwaarde A:
De inhoud per persoon is
`(200h)/x`
m3 en daar geldt voor
`(200h)/x ge 7`
ofwel
`h ge 0,035x`
met vergelijkbare grenslijn.
Voor het linker snijpunt geldt
`0,014x + 1,8 = 2,70`
en dat geeft
`x = 64,3`
.
Voor het rechter snijpunt geldt
`0,014x + 1,8 = 0,0375x`
en dat geeft
`x = 76,6`
.
Voorwaarde B is de strengste voorwaarde in het geval er
`65`
tot en met
`76`
personen in deze werkplaats werken.
(bron: examen wiskunde A in 2003, tweede tijdvak))
Zie figuur. GR met venster `[0, 100]xx[0, 80]` .
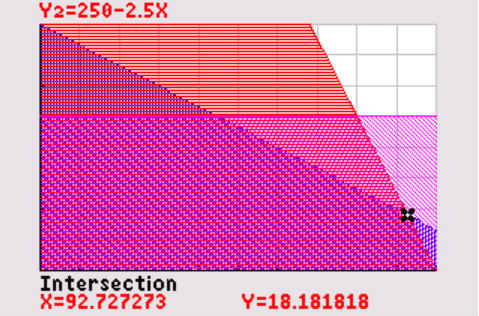
Je ziet dat het minimum zit bij het snijpunt van de lijnen `2x + 3y = 240` en `5x + 2y = 500` , dus in `(1020/11, 200/11)` . Dit maximum is dus `W = 2000 - 1220/11` . Het maximum is `W(0, 0) = 2000` .
Neem `x` het aantal type I en `y` het aantal type II. Dan geldt: `0 le x le 50` , `0 le y le 50` , `x + y le 70` en `x + 1,5y le 110` .
Opbrengst:
`R = 2400x + 3000y`
. De maximale opbrengst is € 198 000,-.
Er worden dan
`20`
type I en
`50`
type II computers gemaakt.
Zeven mensen kunnen `70` computers verpakken. Bij de productie, beschreven in b zijn `95` werknemers bezig. De constructeurs hebben tijd over. Als er meer inpakkers zouden zijn, zou de constructieafdeling meer computers maken.